『液体』や『気体』を扱う『流体力学』では、
文字通り『流れる』という性質があるため、
物理の『力学』と似ているようで違う用語が使われます。
わかる範囲でまとめてみました。
流体力学 物体と流体の違い 流速と流量
- 『流速(りゅうそく』・・流体がどれくらいの速さで流れているか

-
流速 v [m/s] = 距離(l) / 時間 (t)
-
流速[v]・・英語でvelocity(ベロシティ(速度))
- 距離[l]・・英語でlength(レングス(長さ))
- 時間[t]・・英語でtime(タイム(時間))
1秒間に2メートル進んだら [2m/s]になります。
- 『流量(りゅうりょう)』・・単位時間当たりに流れる流体の体積
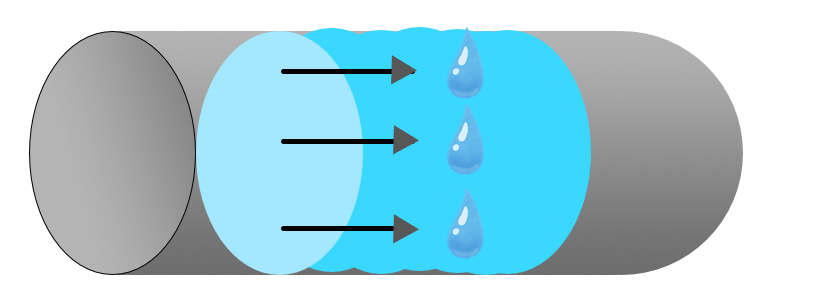
-
流量$$ Q [m^3/s]$$ = 断面積 $$A[m^2]$$ × 流速 v [m/s]
-
流量[Q]・・英語でQuantity(クオンティティ(量))
- 断面積[A]・・英語でArea(エリア)
- 流速[v]・・英語でVelocity(ベロシティ(速度))
断面積が$$3m^3$$ で流速が 2 m/s なら、流量は $$6m^3/s$$ になります。
物体と流体の対応表はこう。
| 物理の力学 | 流体力学 |
|---|---|
| 速度 | 流速 |
| 体積 | 流量 |
| 質量 | 密度 |
『密度』についての関連記事
流体力学の用語 流線・流跡線・流管
流体の中の『流体粒子(りゅうたいりゅうし)』に注目して、
『流体粒子』の動きにも名前がつけられています。
- 『流線(りゅうせん)』・・粒子の動きをつないだ線・・定点観測
こっちはオイラーの方法だそうで。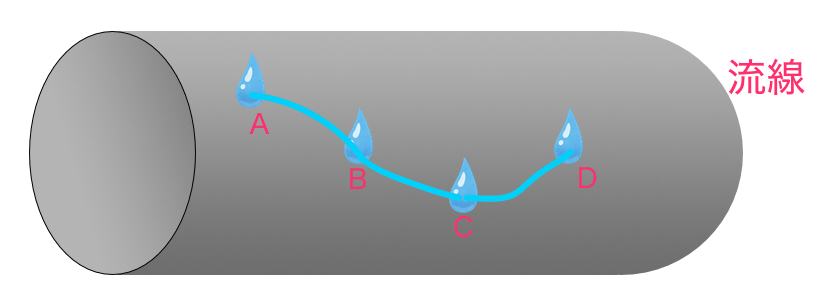
-
『流跡線(りゅうせきせん)』・・1つの粒子の動いた跡・・追いかける
こっちはラグランジュの方法だそうです。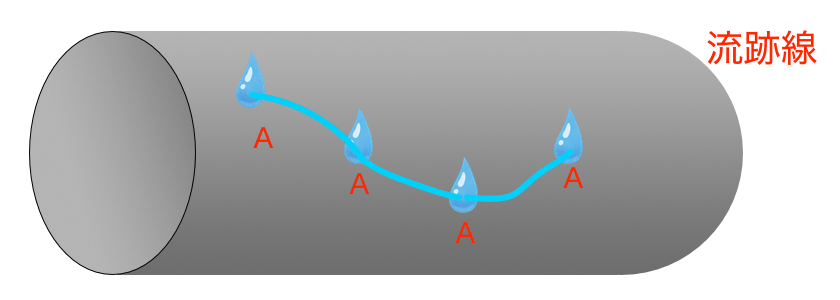
また、『流線』を束ねた『流管』という用語もあります。
- 『流管(りゅうかん)』・・『流線』を束ねた仮想の管・・互いに交差はしない
流体力学 物体と流体の違い 連続の式(質量保存則)

例えばホースで水を流すとすると、
流体の『流量』は、ホースに入る時と出るときでは変わりません。
当たり前すぎてなんだか、なんですが、
これが『流体の質量保存則』であり、『連続の式(れんぞくのしき)』というようです。
例えばホースを細めたりすると、
『断面積』が小さくなるので、その分『流速』が増えるということになります。
- 流量(Q) $$m^3/s$$ = 断面積(A) $$m^2$$ × 流速(v) m/s
・・『断面積』が小さくなると、『流速』は大きくなる(早くなる)
- 体積(V) = 流速×断面積 に 時間 をかけたもの
- 体積(V) = vAt
流量・流速・断面積の関係はこうなります。
- 流量(Q) = vA
- 流量(Q) = v/t = vA
- 流速(v) = Q/A
流体力学 物体と流体の違い ベルヌーイの式(エネルギー保存則)
『エネルギー保存則』も、
『物体』と『流体』でちょっとだけ違って、
『圧力』が加わってきます。
物体のエネルギー保存則
『物理のエネルギー保存則』・・運動エネルギーと位置エネルギーの和は一定
$$\frac{1}{2}mv^2 + mgz = $$一定
- m・・質量(英語でmass)
- z・・高さ(hじゃなくてzなのは3次元を見越してるかも?)
- g・・重力(英語でgravity)
- v・・速度(英語でvelocity)
流体のエネルギー保存則
『流体』の場合、常に流れているので、
『流線』に沿って考える必要があるようです。
『流体のエネルギー保存則』・・運動・圧力・位置3つのエネルギーの和は一定
$$\frac{1}{2}\rho v^2 + p + \rho gz = E [Pa]$$
- $$\rho$$・・密度
- p ・・圧力(英語でpressure(プレッシャー))
- g・・重力(gravity)
- z・・高さ
- E ・・エネルギー(Energy) (単位はパスカル(Pa))
『流体のエネルギー保存則』のことを、『ベルヌーイの式』と呼びます。
ベルヌーイの式は流体の速さと圧力と外力のポテンシャルの関係を記述する式で、力学的エネルギー保存則に相当する。この定理により流体の挙動を平易に表すことができる。ダニエル・ベルヌーイ(Daniel Bernoulli 1700-1782)によって1738年に発表された。Wikipedia:ベルヌーイの定理
エネルギー単位の補足。
$$[Pa] = [\frac{N}{m^2}] = [\frac{N \times m}{m^3}]= [\frac{J}{m^3}]$$
- J・・ジュール エネルギーの単位
流体力学 物体と流体の違い 運動量保存則
『運動量保存則』もまた、
『物体』と『流体』でちょっとだけ違います。
物体の運動量保存則
『物体』の場合。
質量mのボールが速度$$v_1$$で進んでいて、
外部から力(F)が時間($$\Delta t$$)かかった後に衝突して、
速度が速度$$v_2$$に減速したとすると、
こうなります。
$$mv_2 – mv_1 = F\Delta t$$
($$F\Delta t$$ は力積)。
Fに着目するとこうなります。
$$F = \frac{mv_2 – mv_1}{\Delta t}$$
流体の運動量保存則
『流体』の場合は、『流量』『密度』として考える必要があります。
- 密度・・$$\rho [kg/m^3]$$
- 流速・・v [m/s]
- 流量・・Q・・ $$[m^3/s]$$ = 断面積(A) $$[m^2]$$ × 流速(v) [m/s]
-
単位体積あたりの運動量・・ $$\rho v$$
- 単位時間あたりの運動量・・ $$\rho v \times Q$$
$$\rho v_2Q – \rho v_1Q = F$$
- F・・力(Force)・・障害物が与える力など。
流体力学 物体と流体の違いをまとめてみて
『物体』と『流体』では、『流れている』という性質のおかげで、
- 質量保存則・・連続の式
- エネルギー保存則・・ベルヌーイの式
- 運動量保存則
それぞれ微妙に違うということがわかりました。
まだまだ理解不足な箇所があるので、
おって追記・修正していきたいと思います。
『流体力学』関係ではこんな記事も読まれています。
1. 【流体力学】とは 圧力・密度・浮力をまとめてみた【初心者向け】2. 【流体力学】 物体と流体の違いをまとめてみた【流量・連続の式・ベルヌーイなど】
3. 【粘性力】【粘性応力】【粘度】とは わかりやすくまとめてみた【流体力学】
4. 【ベクトル場】と【速度ベクトル】とは わかりやすく【ドラクエのすべる床】
アオキのツイッターアカウント。
















この記事へのコメントはありません。