プログラミングでかっこいい映像がつくれるということで始めた『レイマーチング(Ray Marching』という手法。
前回の記事。
お手本の映像はこちら。
今回は、『立方体(りっぽうたい)』の『距離関数』を使ったり、回転したり、合成させたりしてみました。
『レイマーチング』入門 距離関数 立方体をつくる
『レイマーチング(Ray Marching)』という手法では、
『距離関数』がとても重要な役割になっていて、
描画したい図形によって『距離関数』を変える必要がでてきます。
今回登場したのはこんな『立方体』。
『距離関数』はこちら。
//10. 立方体の距離関数
float box_d(vec3 pos){
return length(max(abs(pos) - vec3(1.0, 1.0, 1.0), 0.0));
}
『距離関数』を立体的に見せるための『法線ベクトル』はこちら。
// 11. 立方体の法線ベクトル
vec3 box_normal(vec3 pos){
float delta = 0.001;
return normalize(vec3(
box_d(pos + vec3(delta, 0.0, 0.0)) - box_d(pos - vec3(delta, 0.0, 0.0)),
box_d(pos + vec3(0.0, delta, 0.0)) - box_d(pos - vec3(0.0, delta, 0.0)),
box_d(pos + vec3(0.0, 0.0, delta)) - box_d(pos - vec3(0.0, 0.0, delta))
));
}
『レイ(Ray)』の判定を、sphere_d からbox_d に変更すれば『立方体』が表示されます。
// 5. Rayの判定
float t = 0.0, d;
for (int i = 0; i < 64; i++ ){ //何回でもok 十分な数
d = box_d(ray.pos); // sphere_d から box_d に変更
カメラがより過ぎてた感があるので 少しカメラを後ろに下げておきます。
//2. 始点の定義 (カメラの姿勢が定まる
vec3 camera_pos = vec3(0.0, 0.0, -8.0); //カメラの位置 -4.0 -> 8.0
『レイマーチング』入門 距離関数 回転させてみる
『立方体』を正面から見ただけでは3D感がでないので、
回転させてみることにします。
物体を回転させるにはいくつかの方法があるのですが、
今回の動画では『回転行列』を使っていました。
『回転行列』を使うと、
決まった法則でかけ算することで、
座標を回転させることができます。
X軸の回転行列はこちら。
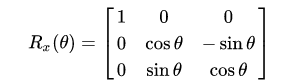
コードにするとこう。
//12. 回転行列(X軸)
mat3 x_axis_rot(float angle){
float c = cos(angle);
float s = sin(angle);
return mat3(1.0, 0.0, 0.0, 0.0, c, -s, 0.0, s, c);
}
『mat3』という型が、3×3の行列を表すようです。
『回転行列』の
- 左上、中上、右上
- 左中、中中、右中
- 左下、中下、右下
という順番で書いています。
Y軸の回転行列はこちら。
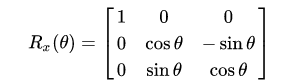
コードはこう。
//12. 回転行列(Y軸)
mat3 y_axis_rot(float angle){
float c = cos(angle);
float s = sin(angle);
return mat3(c, 0.0, s, 0.0, 1.0, 0.0, -s, 0.0, c);
}
実際に使う時はマウス位置のX、Yと連動させています。
//13. 回転行列追加 mat3 rot = x_axis_rot(mouse_pos.x) * y_axis_rot(mouse_pos.y);
『レイ(Ray)』の位置も回転させています。
// 5. Rayの判定
float t = 0.0, d;
for (int i = 0; i < 64; i++ ){ //何回でもok 十分な数
d = box_d(rot * ray.pos); //距離関数から現在の距離を求める // rot をかけ算
if (d < 0.001) { //計算できた距離が十分に0に近かったら
break; //衝突したという判定
//8. 光源が当たる方向を定義(z方向に光があたるように // vec3 light_dir = vec3(0.0, 0.0, 1.0); vec3 light_dir = vec3(- mouse_pos, 1.0); //マウスを光源としてみる vec3 normal = sphere_normal(rot * ray.pos); // rot をかけている

『レイマーチング』入門 距離関数 合成してみる
『距離関数』は単独で使うのはもちろん、
2つの『距離関数』を合成させることもできます。
作成済みの2つの『距離関数』を合成してみます。
- 『球』の『距離関数』
- 『立方体』の『距離関数』
//14. 距離関数はくっつけることができる(差集合、積集合など)
float object_d(vec3 pos){
return max(sphere_d(pos), box_d(pos));
}
min関数 やmax 関数を使うことで合成できるようですが、
うまく雰囲気が掴めてないのでやりながら覚えていく方がいいかなと思います。
立体的に見せるための『法線ベクトル』も作成します。
// 15. 合成距離関数 3D表現(法線ベクトル)
vec3 object_normal(vec3 pos){
float delta = 0.001;
return normalize(vec3(
object_d(pos + vec3(delta, 0.0, 0.0)) - object_d(pos - vec3(delta, 0.0, 0.0)),
object_d(pos + vec3(0.0, delta, 0.0)) - object_d(pos - vec3(0.0, delta, 0.0)),
object_d(pos + vec3(0.0, 0.0, delta)) - object_d(pos - vec3(0.0, 0.0, delta))
));
}
『レイ(Ray)』の判定なども box_d から object_d に変更します。
// 5. Rayの判定
float t = 0.0, d;
for (int i = 0; i < 64; i++ ){ //何回でもok 十分な数
d = object_d(rot * ray.pos); //距離関数から現在の距離を求める // rot をかけ算 // object_dに変更
if (d < 0.001) { //計算できた距離が十分に0に近かったら
break; //衝突したという判定
//8. 光源が当たる方向を定義(z方向に光があたるように // vec3 light_dir = vec3(0.0, 0.0, 1.0); vec3 light_dir = vec3(- mouse_pos, 1.0); //マウスを光源としてみる vec3 normal = object_normal(rot * ray.pos); // rot をかけている // object_dに変更
こんな感じで表示されればOKです。

// 1. 球の距離関数
float sphere_d(vec3 pos){
return length(pos) - 1.5; // 原点にある位置ベクトルから半径を引くと算出できる // 2.0->1.5
}
他にもたくさんの『距離関数』があるようです。
うまく組み合わせたり加工することで、いろんな画像がつくれるようで。
『レイマーチング』入門 距離関数 スムースに合成してみる
『距離関数』2つの合成をよりスムーズにするための方法もあるようです。
// 16. スムース
float smin(float d1, float d2, float k ){
float res = exp(-k * d1) + exp(-k * d2);
return -log(res) / k;
}
どうやら『exp』 はネイピア数で、『log』が対数だそうですが、
なので、素直にコピペしておきます。
こちらの記事により詳細が書かれています。
2019/8/24 追記
『対数』と『ネイピア数』記事書きました。
合成用の距離関数に、作成した『smin関数』を設定します。
//15. 距離関数はくっつけることができる(差集合、積集合など)
float object_d(vec3 pos){
return smin(sphere_d(pos), box_d(pos), 5.0); //sminに変更
//return max(sphere_d(pos), box_d(pos)); //コメントアウト
}
こんな感じに表示されればOKです。
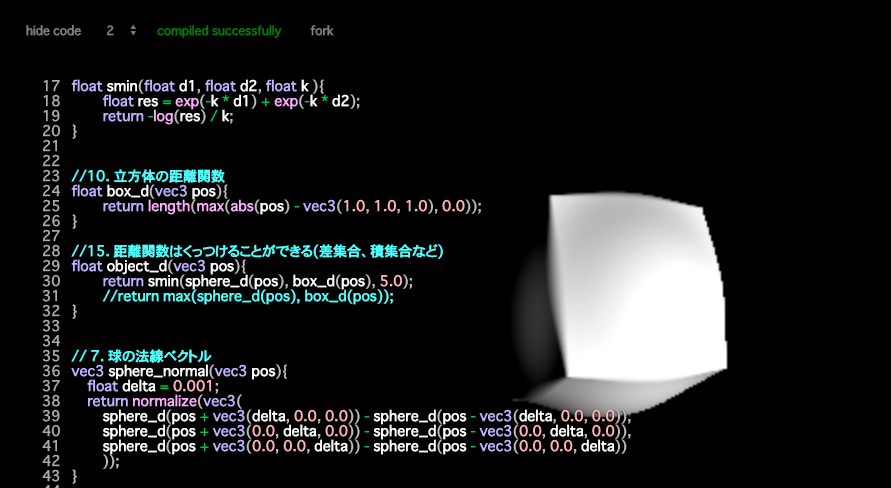
『レイマーチング』入門 距離関数 量産してみる
『レイマーチング(Ray Marching)』では、複数の画像を同時に見せるのも簡単なようで、
『mod』関数を使うと実現できます。
mod関数は数学では『合同式』というそうです。
//16. 距離関数はくっつけることができる(差集合、積集合など)
float object_d(vec3 pos){
vec3 p = mod(pos, 8.0) - 4.0; // mod関数を使う
return smin(sphere_d(p), box_d(p), 5.0); // 引数にpをつける
//return max(sphere_d(pos), box_d(pos));
}
これだけでこんな映像が表現されます。
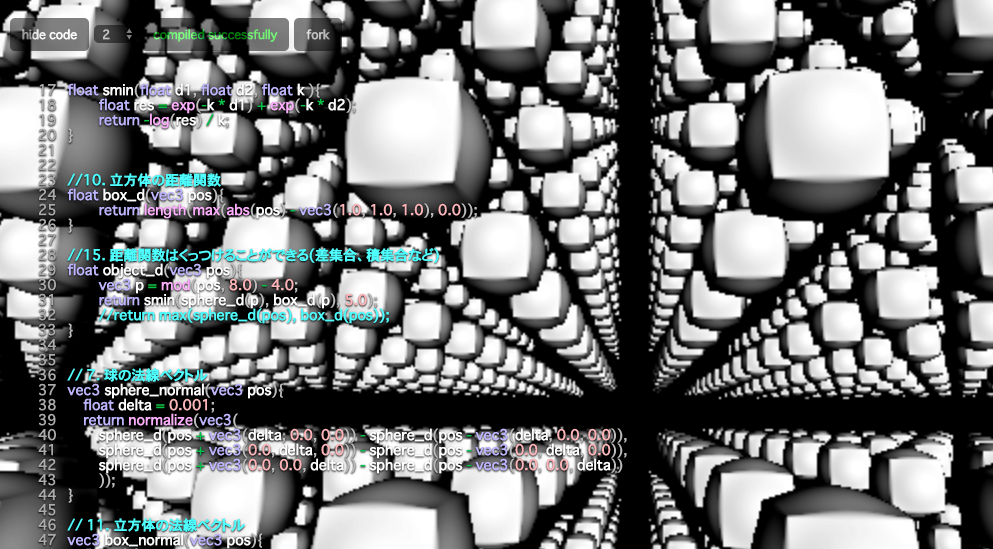
カメラの動きを調整することで、
前に進むような映像もつくることができます。
//2. 始点の定義 (カメラの姿勢が定まる
vec3 camera_pos = vec3(0.0, 0.0, -8.0 + time * 5.0); //カメラの位置 // timeの5倍を足している
vec3 camera_up = vec3(0.0, 1.0, 0.0); //カメラの上向きベクトル
vec3 camera_dir = vec3(0.0, 0.0, 1.0); //カメラの前向きベクトル
vec3 camera_side = cross(camera_up, camera_dir); //カメラの横向きベクトル (上向きベクトルと前向きベクトルの外積
完成版のコードはこちら。
#ifdef GL_ES
precision mediump float;
#endif
#extension GL_OES_standard_derivatives : enable
uniform float time;
uniform vec2 mouse;
uniform vec2 resolution;
// 1. 球の距離関数
float sphere_d(vec3 pos){
return length(pos) - 1.5; // 原点にある位置ベクトルから半径を引くと算出できる // 2.0->1.5
}
//10. 立方体の距離関数
float box_d(vec3 pos){
return length(max(abs(pos) - vec3(1.0, 1.0, 1.0), 0.0));
}
// 16. スムース
float smin(float d1, float d2, float k ){
float res = exp(-k * d1) + exp(-k * d2);
return -log(res) / k;
}
//14. 距離関数はくっつけることができる(差集合、積集合など)
float object_d(vec3 pos){
vec3 p = mod(pos, 8.0) - 4.0; // mod関数を使う
return smin(sphere_d(p), box_d(p), 5.0); // 引数にpをつける
//return max(sphere_d(pos), box_d(pos));
}
// 7. 球の法線ベクトル
vec3 sphere_normal(vec3 pos){
float delta = 0.001;
return normalize(vec3(
sphere_d(pos + vec3(delta, 0.0, 0.0)) - sphere_d(pos - vec3(delta, 0.0, 0.0)),
sphere_d(pos + vec3(0.0, delta, 0.0)) - sphere_d(pos - vec3(0.0, delta, 0.0)),
sphere_d(pos + vec3(0.0, 0.0, delta)) - sphere_d(pos - vec3(0.0, 0.0, delta))
));
}
// 11. 立方体の法線ベクトル
vec3 box_normal(vec3 pos){
float delta = 0.001;
return normalize(vec3(
box_d(pos + vec3(delta, 0.0, 0.0)) - box_d(pos - vec3(delta, 0.0, 0.0)),
box_d(pos + vec3(0.0, delta, 0.0)) - box_d(pos - vec3(0.0, delta, 0.0)),
box_d(pos + vec3(0.0, 0.0, delta)) - box_d(pos - vec3(0.0, 0.0, delta))
));
}
// 15. 合成距離関数 3D表現(法線ベクトル)
vec3 object_normal(vec3 pos){
float delta = 0.001;
return normalize(vec3(
object_d(pos + vec3(delta, 0.0, 0.0)) - object_d(pos - vec3(delta, 0.0, 0.0)),
object_d(pos + vec3(0.0, delta, 0.0)) - object_d(pos - vec3(0.0, delta, 0.0)),
object_d(pos + vec3(0.0, 0.0, delta)) - object_d(pos - vec3(0.0, 0.0, delta))
));
}
//3. Rayの定義 (構造体)
struct Ray{
vec3 pos; //Rayの現在の座標
vec3 dir; //Rayの進行方向
};
//12. 回転行列(X軸)
mat3 x_axis_rot(float angle){
float c = cos(angle);
float s = sin(angle);
return mat3(1.0, 0.0, 0.0, 0.0, c, -s, 0.0, s, c);
}
//12. 回転行列(Y軸)
mat3 y_axis_rot(float angle){
float c = cos(angle);
float s = sin(angle);
return mat3(c, 0.0, s, 0.0, 1.0, 0.0, -s, 0.0, c);
}
void main( void ) {
vec2 pos = ( gl_FragCoord.xy * 2.0 - resolution) / max(resolution.x, resolution.y); //現在の画素位置を0.0-1.0に正規化
vec2 mouse_pos = (mouse - 0.5) * 2.0;
mouse_pos.y *= resolution.y / resolution.x;
//2. 始点の定義 (カメラの姿勢が定まる
vec3 camera_pos = vec3(0.0, 0.0, -8.0 + time * 5.0); //カメラの位置
vec3 camera_up = vec3(0.0, 1.0, 0.0); //カメラの上向きベクトル
vec3 camera_dir = vec3(0.0, 0.0, 1.0); //カメラの前向きベクトル
vec3 camera_side = cross(camera_up, camera_dir); //カメラの横向きベクトル (上向きベクトルと前向きベクトルの外積
// 4. Rayの設定
Ray ray; //ここはインスタンスか
ray.pos = camera_pos; //Rayの初期位置
ray.dir = normalize(pos.x * camera_side + pos.y * camera_up + camera_dir); // Rayの進行方向はカメラの姿勢から求めることができる
//13. 回転行列追加
mat3 rot = x_axis_rot(mouse_pos.x) * y_axis_rot(mouse_pos.y);
// 5. Rayの判定
float t = 0.0, d;
for (int i = 0; i < 64; i++ ){ //何回でもok 十分な数
d = object_d(rot * ray.pos); //距離関数から現在の距離を求める
if (d < 0.001) { //計算できた距離が十分に0に近かったら
break; //衝突したという判定
}
t += d; //当たらなかったら
ray.pos = camera_pos + t * ray.dir; //rayの座標更新 どれだけrayを進めるかというと最も近いオブジェクトまでの距離(突き抜け防止
}
//8. 光源が当たる方向を定義(z方向に光があたるように
// vec3 light_dir = vec3(0.0, 0.0, 1.0);
vec3 light_dir = vec3(- mouse_pos, 1.0); //マウスを光源としてみる
vec3 normal = object_normal(rot * ray.pos);
float l = dot(normal, - light_dir); //法線ベクトルと光源のベクトルの内積(dot)
//6. あたったら色を変える
//9, 色を内積の値にする
if (d < 0.001) {
gl_FragColor = vec4(l, l, l, 1.0);
} else {
gl_FragColor = vec4(0);
}
}
ここに貼り付けると動くと思います。
※そこそこ負荷が高いので古いパソコンだと動かないかも、です。
『レイマーチング』入門 まとめ
先人のありがたい動画のおかげで、『レイマーチング(Ray Marching)』のたくさんの知識をまとめてえることができました。
もちろんまだまだわからないことがたくさんありはしますが、
『守破離』の精神で、まずはコピーしつつ解読してネタを増やしていきたいなと思います。
『GLSL(シェーディング)』関係ではこんな記事も読まれています。
1. 【GLSL】プログラムでかっこいい映像をつくりたい! 〜『TouchDesigner』を見据えて2. 【WebGL】入門 わかりやすく【図解】してみた
3. 【OpenGL】と【DirectX】のバージョンをまとめてみた【シェーダーメイン】【初心者向け】
4. 【GLSL(シェーディング)】でよく使う関数とユーザー関数のまとめ※随時更新
5. 【GLSL】プログラムでかっこいい映像をつくるには『レイマーチング』なるものを覚えればいいらしい
6. 【GLSL】『レイマーチング』入門その1 距離関数とレイとカメラの設定
7. 【GLSL】『レイマーチング』入門(2) 立体的に見せる方法〜光の反射は『内積』で〜
8. 【GLSL】『レイマーチング』入門(3) 距離関数を使ってみる・回転・合成・量産
9. 【TouchDesigner】で『GLSL』を使う方法まとめ【画像あり】
10. 【TouchDesigner】『GLSL MAT』の使い方 3次元でぐりぐり動かしてみる
11. 【GLSL】波のつくり方簡易まとめ。波もプログラムでつくれます【コピペスタイル】
アオキのツイッターアカウント。


















この記事へのコメントはありません。