プログラミングでかっこいい映像をつくる方法の一つに、
『レイマーチング(Ray Marching』なる技術があることを知りました。
前回の記事
前回の記事で円を表示することができたので、
次は光をあてて、明るい箇所と暗い箇所をつくり、
より立体的に見えるようにしています。
『レイマーチング』入門〜立体的に見せる方法
参考にさせていただいている動画はこちら。
今回の完成画像はこちら。
『レイ(光源)』が当たっている球の中心が白く表示されて、
外側に行くほど暗くなっているのがわかるかと思います。
この画像をつくるためには、
『光源ベクトル(レイ)』と、
『光源ベクトル(レイ)』の接線に垂直な『法線ベクトル』との『内積(ないせき)』を求める必要があります。
と思ったのでググりにググってイメージをつくってみました。
『レイマーチング』入門〜立体的に見せるための『法線ベクトル』
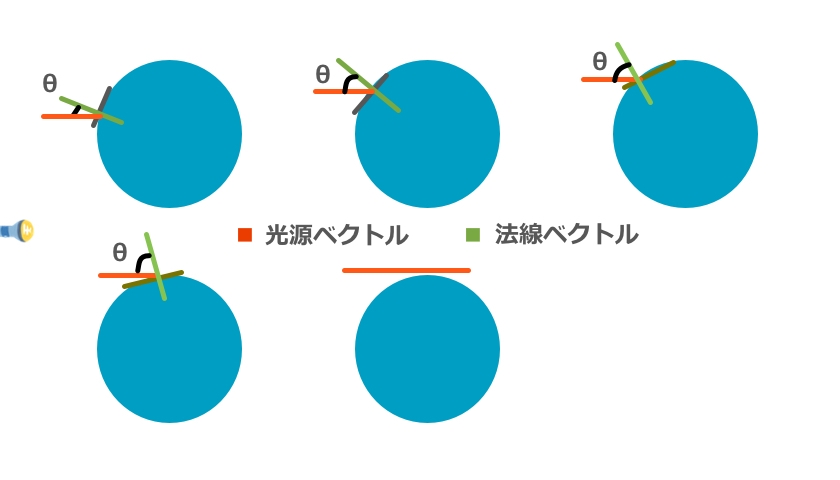
イメージの左側に『光源』があって、
球に向かってまっすぐ『レイ(光源ベクトル)』が飛んでいきます。
『レイ(光源ベクトル)』が球に接する箇所が『接線(グレーの線)』で、
『接線』と垂直に交わる線を『法線(ほうせん)』といいます。
『法線』は英語で 『normal line』だそうです。
球の中心に近いほど、
『レイ(光源ベクトル)』と『法線ベクトル』の角度が小さくなって、
球の上側(下側)に行くほど、
『レイ(光源ベクトル)』と『法線ベクトル』の間の角度が大きくなっていきます。
角度がどれくらい大きくなるかというと、
『レイ(光源ベクトル)』と『法線ベクトル』の角度が90度(または-90度)になったら、
『レイ(光源ベクトル)』は球に接していない、ということになります。
(イメージの下の段中央の図)
『レイマーチング』入門〜『法線ベクトル』は『偏微分』で求まるそう
『法線ベクトル』を求めるコードがこちら。
// 7. 球の法線ベクトル
vec3 sphere_normal(vec3 pos){
float delta = 0.001;
return normalize(vec3(
sphere_d(pos + vec3(delta, 0.0, 0.0)) - sphere_d(pos - vec3(delta, 0.0, 0.0)), //X
sphere_d(pos + vec3(0.0, delta, 0.0)) - sphere_d(pos - vec3(0.0, delta, 0.0)), //Y
sphere_d(pos + vec3(0.0, 0.0, delta)) - sphere_d(pos - vec3(0.0, 0.0, delta)) //Z
));
}
こちらもいろいろググってみるとどうやら、
『法線ベクトル』は『偏微分(へんびぶん)』で求まるそうで。
と調べてみると、
いくつか変数があった時に、
求めたい変数だけを微分して、他は定数で計算することだそう。
XならXだけ微分して、YとZは定数(今回は0)としてそれぞれ計算するようです。
そう言われると確かにこのコード。
sphere_d(pos + vec3(delta, 0.0, 0.0)) - sphere_d(pos - vec3(delta, 0.0, 0.0)), //X sphere_d(pos + vec3(0.0, delta, 0.0)) - sphere_d(pos - vec3(0.0, delta, 0.0)), //Y sphere_d(pos + vec3(0.0, 0.0, delta)) - sphere_d(pos - vec3(0.0, 0.0, delta)) //Z
vec3の中が、deltaと0.0、0.0 になっていて、
deltaが1つずつ右にずれて書かれています。
X、Y、Zそれぞれで、2点間の距離を出しているようです。
微分の参考記事
名前がしっくりこなくて英語版を調べてみると、
『偏微分』は英語で『Partial differential(パーシャルディファレンシャル)』で、
『Partial(パーシャル)』は一部分という意味なので、
部分的に微分するって理解でよさそう。
と思い改めて動画を見てみると、
というような説明で。
うーん、わかるようでわからん。
ググってみるに関連する情報はありそうですが、
なかなか難しいようなので、とりあえず次に進むことに。
参考記事
2019/8/12 追記
『ベクトル分析 勾配』の記事を書きました。
改めて、『法線ベクトル』を求めるコードがこちら。
// 7. 球の法線ベクトル
vec3 sphere_normal(vec3 pos){
float delta = 0.001;
return normalize(vec3(
sphere_d(pos + vec3(delta, 0.0, 0.0)) - sphere_d(pos - vec3(delta, 0.0, 0.0)), //X
sphere_d(pos + vec3(0.0, delta, 0.0)) - sphere_d(pos - vec3(0.0, delta, 0.0)), //Y
sphere_d(pos + vec3(0.0, 0.0, delta)) - sphere_d(pos - vec3(0.0, 0.0, delta)) //Z
));
}
球の『法線ベクトル』なので『sphere_normal』という関数名にしています。
それぞれの意味は以下になります。
- vec3はベクトル3(x,y,z 3つの値をもつ)
- sphere(スフィア)は英語で球
- normal(ノーマル)が法線ベクトルの意味
-
float(フロート)は小数点型
- delta(デルタ)はほんのちょっとの値
- return(リターン)は関数の戻り値
- normalize(ノーマライズは正規化(ベクトルを1に最適化)
- sphere_dは球の距離関数 (前回の記事を参照)
これで、法線ベクトルが求まることになります。
『レイマーチング』入門〜『法線ベクトル』との『内積』を求める
『法線ベクトル』がなんとなく計算できたので、
次は『光源ベクトル』と『法線ベクトル』の『内積(ないせき)』を求めます。
『内積』のイメージ図はこちら。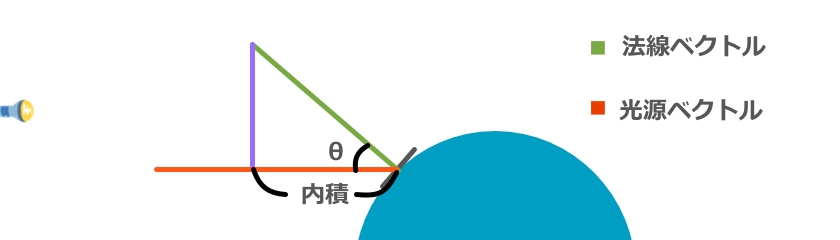
球に触れる接点から、
『法線ベクトル(緑)』からまっすぐ下に下ろした箇所までの長さを
『内積(ないせき)』というそうです。
『内積(ないせき)』の式はこちら。
内積 = $$ |a||b|cosθ $$
参考記事
【内積とは】ベクトルの内積の意味や公式・計算方法を知って大学合格へ!
改めてこちらの図をば。
cosθ(コサイン)が入っているので、
『光源ベクトル』と『法線ベクトル』の角度が90度だと、内積は0になります。
『光源ベクトル』と『法線ベクトル』の角度が-90度でも、内積は0になります。
cosθ(コサイン)の参考記事
なので、
-90度 < θ < 90度 の範囲であれば内積が0より大きくなって、
光が当たっているということになります。
コードはこちら。
//8. 光源が当たる方向を定義(z方向に光があたるように
vec3 light_dir = vec3(0.0, 0.0, 1.0);
vec3 normal = sphere_normal(ray.pos);
float l = dot(normal, - light_dir); //法線ベクトルと光源のベクトルの内積(dot)
//6. あたったら色を変える
//9, 色を内積の値にする
if (d < 0.001) {
gl_FragColor = vec4(l, l, l, 1.0);
} else {
gl_FragColor = vec4(0);
}
光源の方向と、法線ベクトルを定義して、float l に『内積』を設定しています。
float l = dot(normal, - light_dir); //法線ベクトルと光源のベクトルの内積(dot)
『内積』は英語で『dot product』なのでdot関数だそうです。
『レイ』がZ軸のマイナス方向からあたっているので、マイナスをつけていると思われます。
ちなみに、マウスがある場所を光源にするには、こちらのコードに変更すればOKです。
//8. 光源が当たる方向を定義(z方向に光があたるように
// vec3 light_dir = vec3(0.0, 0.0, 1.0); //コメントアウト
vec3 light_dir = vec3(- mouse_pos, 1.0); //マウスを光源としてみる
vec3 normal = sphere_normal(ray.pos);
float l = dot(normal, - light_dir); //法線ベクトルと光源のベクトルの内積(dot)
//6. あたったら色を変える
//9, 色を内積の値にする
if (d < 0.001) {
gl_FragColor = vec4(l, l, l, 1.0);
} else {
gl_FragColor = vec4(0);
}
全体のコードはこちら。
#ifdef GL_ES
precision mediump float;
#endif
#extension GL_OES_standard_derivatives : enable
uniform float time;
uniform vec2 mouse;
uniform vec2 resolution;
// 1. 球の距離関数
float sphere_d(vec3 pos){
return length(pos) - 2.0; // 原点にある位置ベクトルから半径を引くと算出できる
}
// 7. 球の法線ベクトル
vec3 sphere_normal(vec3 pos){
float delta = 0.001;
return normalize(vec3(
sphere_d(pos + vec3(delta, 0.0, 0.0)) - sphere_d(pos - vec3(delta, 0.0, 0.0)),
sphere_d(pos + vec3(0.0, delta, 0.0)) - sphere_d(pos - vec3(0.0, delta, 0.0)),
sphere_d(pos + vec3(0.0, 0.0, delta)) - sphere_d(pos - vec3(0.0, 0.0, delta))
));
}
//3. Rayの定義 (構造体)
struct Ray{
vec3 pos; //Rayの現在の座標
vec3 dir; //Rayの進行方向
};
void main( void ) {
vec2 pos = ( gl_FragCoord.xy * 2.0 - resolution) / max(resolution.x, resolution.y); //現在の画素位置を0.0-1.0に正規化
vec2 mouse_pos = (mouse - 0.5) * 2.0;
mouse_pos.y *= resolution.y / resolution.x;
//2. 始点の定義 (カメラの姿勢が定まる
vec3 camera_pos = vec3(0.0, 0.0, -4.0); //カメラの位置
vec3 camera_up = vec3(0.0, 1.0, 0.0); //カメラの上向きベクトル
vec3 camera_dir = vec3(0.0, 0.0, 1.0); //カメラの前向きベクトル
vec3 camera_side = cross(camera_up, camera_dir); //カメラの横向きベクトル (上向きベクトルと前向きベクトルの外積
// 4. Rayの設定
Ray ray; //ここはインスタンスか
ray.pos = camera_pos; //Rayの初期位置
ray.dir = normalize(pos.x * camera_side + pos.y * camera_up + camera_dir); // Rayの進行方向はカメラの姿勢から求めることができる
// 5. Rayの判定
float t = 0.0, d;
for (int i = 0; i < 64; i++ ){ //何回でもok 十分な数
d = sphere_d(ray.pos); //距離関数から現在の距離を求める
if (d < 0.001) { //計算できた距離が十分に0に近かったら
break; //衝突したという判定
}
t += d; //当たらなかったら
ray.pos = camera_pos + t * ray.dir; //rayの座標更新 どれだけrayを進めるかというと最も近いオブジェクトまでの距離(突き抜け防止
}
//8. 光源が当たる方向を定義(z方向に光があたるように
// vec3 light_dir = vec3(0.0, 0.0, 1.0);
vec3 light_dir = vec3(- mouse_pos, 1.0); //マウスを光源としてみる
vec3 normal = sphere_normal(ray.pos);
float l = dot(normal, - light_dir); //法線ベクトルと光源のベクトルの内積(dot)
//6. あたったら色を変える
//9, 色を内積の値にする
if (d < 0.001) {
gl_FragColor = vec4(l, l, l, 1.0);
} else {
gl_FragColor = vec4(0);
}
}
このコードをGLSLオンラインエディタにコピペすればOKです。
こんな画像が表示されればOKです。

『レイマーチング』入門その2 まとめ
『レイマーチング(Ray Marching)』を調べるうちに、
いろんな数学知識が必要になってきました。
- ベクトル
- 三角関数
- 法線ベクトル
- 微分(偏微分)
- 内積
- 外積
学生時代ろくに勉強してなかった身としてはなかなかハードですが、
ずーーっとググって文章を読んで理解しようとしていくうちに、
徐々にではありますがわかってきたような気がしています。
『3Dプログラミング』はこれからますます需要が増えてくると思いますし、
実はこれらの数学知識は『機械学習』『統計学』『経済学』なんかでも応用できるようなので、
まるっとまとめてちょっとずつでも覚えていければと思います。
『GLSL(シェーディング)』関係ではこんな記事も読まれています。
1. 【GLSL】プログラムでかっこいい映像をつくりたい! 〜『TouchDesigner』を見据えて2. 【WebGL】入門 わかりやすく【図解】してみた
3. 【OpenGL】と【DirectX】のバージョンをまとめてみた【シェーダーメイン】【初心者向け】
4. 【GLSL(シェーディング)】でよく使う関数とユーザー関数のまとめ※随時更新
5. 【GLSL】プログラムでかっこいい映像をつくるには『レイマーチング』なるものを覚えればいいらしい
6. 【GLSL】『レイマーチング』入門その1 距離関数とレイとカメラの設定
7. 【GLSL】『レイマーチング』入門(2) 立体的に見せる方法〜光の反射は『内積』で〜
8. 【GLSL】『レイマーチング』入門(3) 距離関数を使ってみる・回転・合成・量産
9. 【TouchDesigner】で『GLSL』を使う方法まとめ【画像あり】
10. 【TouchDesigner】『GLSL MAT』の使い方 3次元でぐりぐり動かしてみる
11. 【GLSL】波のつくり方簡易まとめ。波もプログラムでつくれます【コピペスタイル】
アオキのツイッターアカウント。




















この記事へのコメントはありません。