『3Dプログラミング』に取り組むうちに目にするようになってきた『ベクトル解析』。
『3Dプログラミング』に限らず『工学系』の業界なら必須とも言われている『ベクトル解析』。
『ベクトル解析』には3つ種類があります。
- 勾配(grad)
- 発散(div)
- 回転(rot)
なかなかわかりやすい記事がなかったのでまとめることに。
この記事では『勾配(こうばい)』についてまとめています。
ベクトル解析 勾配(grad) についてわかりやすく グラフをつくってみる
『勾配(こうばい)』は、傾きや斜面という意味になります。
- 勾配(こうばい)・・英語でgradient(グラディエント)。略してgrad(グラッド)
グラフで見た方がわかりやすいのでさっそくグラフをつくってみます。
『Mac』だと標準で『Grapher』というアプリがあるので起動して、
今回は、$$ z = x+ \frac{1}{2}y $$ というグラフをつくってみます。
『X』と『Y』2つの変数があるので、
$$ f(x,y) = x+ \frac{1}{2}y $$
ともかけます。
- x・・横軸
- y・・手前-奥 に向かう軸
- z ・・高さ
『X』と『Y』の値が決まれば高さが決まると。
見るからに斜面なグラフがつくれました。
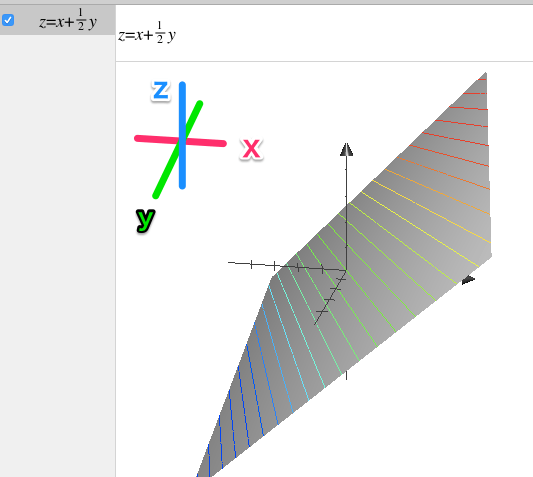
適当に数値を入れて計算してみます。
- Xが1、yも1・・Zは1.5
- Xが10、Yが20・・Zは20
という具合ですね。
ベクトル解析 勾配(grad) についてわかりやすく もっとも坂が急になるのは?

このグラフで、もっとも坂が急になる方向を考えてみます。
例えば『X』と『Y』が1の地点から、『X方向』にだけ10進むとすると、
- Xが10、Yは1のまま・・Zは10.5
になります。
例えば『X』と『Y』が1の地点から、『Y方向』にだけ10進むとすると、
- Xは1のまま、Yは10・・Zは6
になります。
もし『X』と『Y』が1の地点から、『X方向』にも『Y方向』にも10進むとすると、
- Xは11、Yも11・・Zは16.5
になります。
『X方向』や『Y方向』にだけ進むよりも、
『X』と『Y』どちらとも進んだ方が、
より高さが高くなる=斜面が急になるという事になります。
ベクトル解析 勾配(grad) についてわかりやすく 等高線の垂直が勾配
『X方向』や『Y方向』にだけ進むよりも、
『X』と『Y』どちらとも進んだ方が、
より高さが高くなる=斜面が急になるという事はわかったものの、
果たして、『X』と『Y』をどれくらいで進めたらええのかな?
という疑問がでてくるのは当然で、そのヒントが『等高線』になります。
- 等高線・・高さが同じ線
『Mac』の『Grapher』には『等高線(とうこうせん)』を表示する機能がついています。
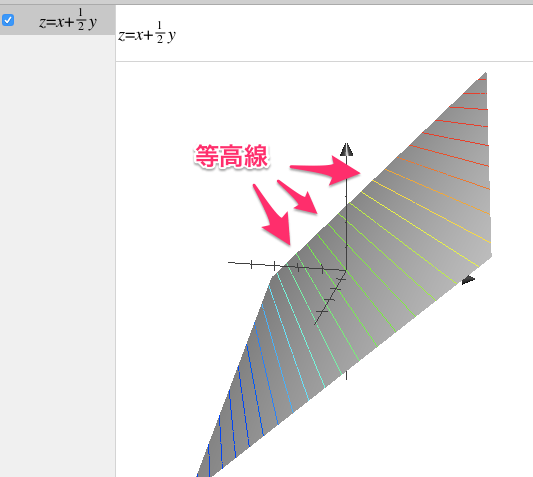
例えば高さが10になる条件はいくつかあります。
- Xが9.5、Yが1・・Zは10
- Xが9、Yが2・・Zは10
- Xが8、Yが4・・Zは10
- Xが7、Yが6・・Zは10
- 小数点含めて小刻みに計算すると等高線が引けることになります。
となると、1番高さが高くなる向きは、
等高線の垂直方向に進めばOK、ということになります。
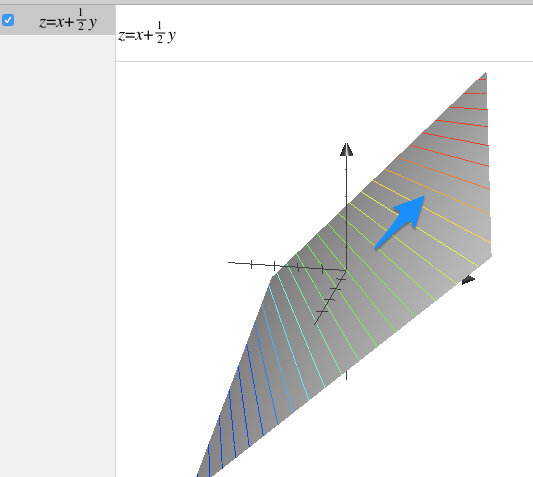
実は、等高線の垂直方向を示しているのが『勾配(grad)』なんです。
ベクトル解析 勾配(grad) についてわかりやすく 勾配の式と偏微分
『X』と『Y』どちらにも進み、
さらに『等高線』の垂直方向が最も高さが高くなる=斜面が急になると。
それを式で表したのが、『勾配(grad)』になります。
『勾配(grad)』の式は以下。
$$ grad f = (\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}) $$
ぱっと見なんじゃこりゃなんですが、
書いてある意味は先ほどと同様、
『X』と『Y』どっちにも進むのが一番変化するよという意味です。
この記号『$$ \partial $$』は『ラウンド』と呼んで、
『偏微分(へんびぶん)』を表します。
※ラウンド、ディー、パーシャルなどいくつか呼び方があります。
『偏微分』は日本語だとわかりづらいんですが、
英語にすると『partial(一部分)』という意味を表していて、
まずXだけを微分して、(Yは0として扱う)
次にYだけを微分します。(Xは0として扱う)
微分についての参考記事
先ほどグラフを作った関数を『偏微分』すると・・・
$$ f(x,y) = x+ \frac{1}{2}y $$
- xだけに注目して微分すると、xは1乗なので1になります。yは0扱い。
- yだけに注目して微分すると、yは1乗なので1になります。xは0扱い。
ということで、
$$ grad f = (1,\frac{1}{2}) $$
になります。
そうなんですよね、『1次関数』だと『x』と『y』が消えちゃうだけになります。
もし、xを2乗として『2次関数』の状態で『偏微分』すると・・・
式: $$ f(x,y) = x^2+ \frac{1}{2}y $$
グラフ(『2次関数』なのでグイーンと上がっていく。)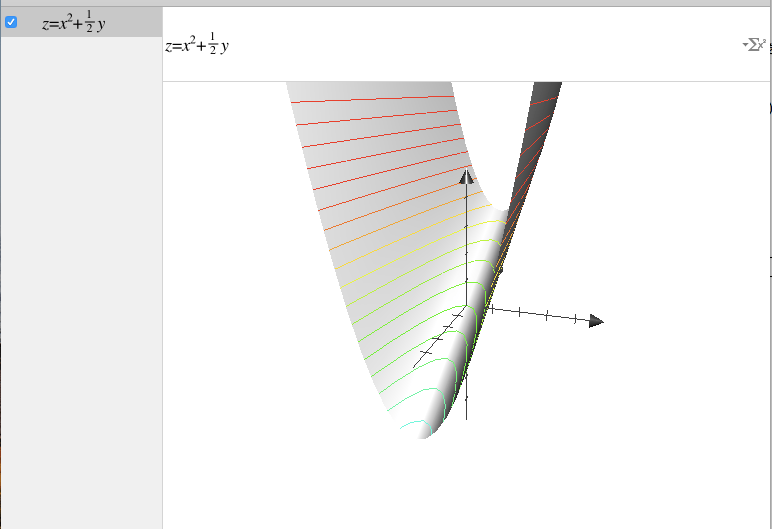
- xだけを注目して微分すると、xは2乗なので2xになります。yは0扱い。
- yだけを注目して微分すると、yは1乗なので1になります。xは0扱い。
ということで、
$$ grad f = (2x, \frac{1}{2}) $$
になります。
微分についての参考記事
ベクトル解析 勾配(grad) についてわかりやすく 3変数も同様に
これまでは『X』と『Y』が決まれば『Z(高さ)』が決まる式を考えていましたが、
3次元空間だと3つの変数をとるケースもあります。
例えば温度。
『X』と『Y』と『Z』3つの値が決まった段階で、その地点の温度が決まると。
この場合、『X』『Y』『Z』『温度』と4つの情報が必要なので、
残念ながらグラフには表現できないのですが、
考え方は同じになるので、
もっとも温度が高くなる方向が『勾配(grad)』になります。
式はこう。
$$ grad f = (\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}, \frac{\partial f}{\partial z}) $$
ベクトル解析 勾配(grad) についてわかりやすく ナブラ
当時の数学者たちが、
何度も何度も『偏微分』の式を書いて手が疲れちゃっていた・・のかはわかりませんが、
『偏微分』の式を簡単に、記号で表す事もできるように考えました。
それが、『$$ \nabla $$ (ナブラ)』。
式にするとこう。
2変数版。
$$ \nabla = (\frac{\partial }{\partial x},\frac{\partial }{\partial y}) $$
3変数版。
$$ \nabla = (\frac{\partial}{\partial x},\frac{\partial}{\partial y}, \frac{\partial}{\partial z}) $$
逆三角形一つで、
2次元ならxとyの『偏微分』を、
3次元ならx,y,zの『偏微分』をまとめて表現しています。
『勾配(grad)』の式も、『$$ \nabla $$ (ナブラ)』を使って書き換えることができます。
『勾配(grad)』2変数版。
$$ grad f = \nabla f = (\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}) $$
『勾配(grad)』3変数版。
$$ grad f = \nabla f = (\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}, \frac{\partial f}{\partial z}) $$
ベクトル解析 勾配(grad) についてわかりやすく 余談 法線ベクトル
ここは余談なんですが、
『斜面』に対して垂直な向きを『法線』と呼びます。
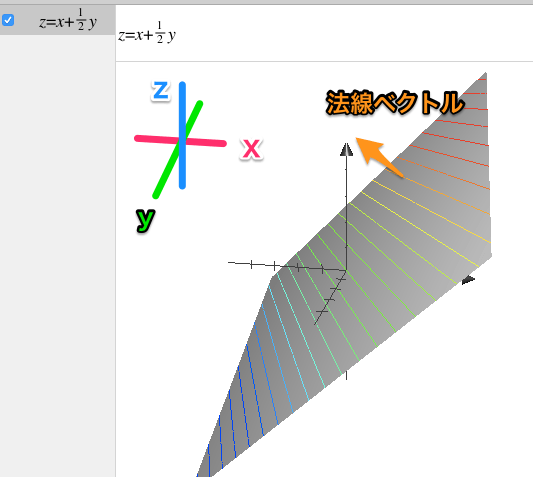
『3Dプログラミング』では光の当たり方を計算するために『法線』がしょっちゅう使われまして、
『法線』を求めるために『勾配(偏微分)』が使われています。
参考記事
ベクトル解析 勾配(grad) についてわかりやすくまとめてみた感想
これまでの日常生活ではほとんど触れてこなかった『ベクトル解析』ですが、
『3Dプログラミング』に取り組むにつれ、よく目にするようになっていました。
『チームラボ』の本にもがっつり『ベクトル解析』が書かれています。
(正確には『ベクトル解析』が前提の『ナビエストークス』方程式が書かれています。さらにムズカシイ・・)
『チームラボ』の『メディアアート』映像。
『ベクトル解析』をしっかりモノにして、
キレイで楽しめる映像がつくれたらなと思っています。
PS.
こちらの本を参考にしつつ記事を書きました。読みやすいのでぜひ。
『数学・物理』関係ではこんな記事も読まれています。
1. 【P5.js】初心者向けの動画をリリースしました(プログラミング×数学物理)【Udemy】2. 【ベクトル】をわかりやすくするコツ〜『ベクトル』はただの数値の組み合わせです(4)【P5.js】
3. プログラムで数学も身につく 一石四鳥なクリエイティブコーディング
4. 【三角関数】の使い方〜わかりやすさ重視でまとめてみた【動画あり】
5. 【ラジアン】とは わかりやすくまとめてみた【初心者向け】
6. 【図解】波の用語や動きをプログラムも交えてまとめてみる【数学&物理】
7. 【微分】とは わかりやすくまとめてみた〜めっちゃすごいわり算【初心者向け】
8. 【シグマ(∑)】計算をわかりやすくまとめてみた【エクセルのsum】【初心者向け】
9. 【極座標 】とは【直交座標 】との違いや変換方法についてまとめてみた
10. 【虚数】【複素数】とは わかりやすくまとめてみた【初心者向け】
11. 【指数】とは わかりやすくまとめてみた【初心者向け】
12. 【対数】とは わかりやすくまとめてみた【初心者向け】
13. 順列・組み合わせ・階乗とは わかりやすくまとめてみた【数学】
14. 【確率(加法定理)】とは わかりやすくまとめてみた【初心者向け】
15. 【ベクトル場】と【速度ベクトル】とは わかりやすく【ドラクエのすべる床】
↓ ここから下は物理関連
1. プログラムで【加速度】をわかりやすくするために実際に動かしてみる(5)【P5.js】
2. 【流体力学】とは 圧力・密度・浮力をまとめてみた【初心者向け】
↓ ここから下はちょいムズカシイ
1. 【ネイピア数】とは わかりやすくまとめてみた【自然対数の底(e)】
2. 【ベクトル解析 勾配(grad)】わかりやすくまとめてみた
3. 【ベクトル解析 発散(div)】わかりやすくまとめてみた
4. 【テイラー展開】をわかりやすくまとめてみた【おすすめ動画あり】
アオキのツイッターアカウント。
















この記事へのコメントはありません。