2020/6/5追記 ラジアンに関する動画を追加しました。

というわけで、いろいろググってまとめてみることにしました。

ラジアンとは わかりやすく・・そもそもなぜに360度？

角度がぐるっと一周回ったら360度というのは、

小学生の頃から何度も教わってきたんですが、

と調べてみると、古代メソポタミア時代までさかのぼるそうで。

はっきりとしたことは分かっていませんが、メソポタミアの人達が勝手に決めたそうです。
当時の計測方法では１年が360日くらい、ということが分かっていて、ちょうど色んな数字で割りやすい数字として、360を一周にすると決められたと言います。

つまり、そのときメソポタミアの誰かが、
「やっぱ362°にしようぜ。」
と言ってたら、一回転は362°になっていたのかもしれません。

参照元：一回転ってなんで360度なの？その意外な理由

思えば、

• 1年は365日。太陽の周りを地球が一周する期間。
• 角度の一周は360。

・・

・・

・・ん・・？

と思ったり。

そこで登場するのが、半径を意味するラテン語『radius』に由来する『ラジアン』です。

ラジアンとは わかりやすく ぴったり一周させたくて

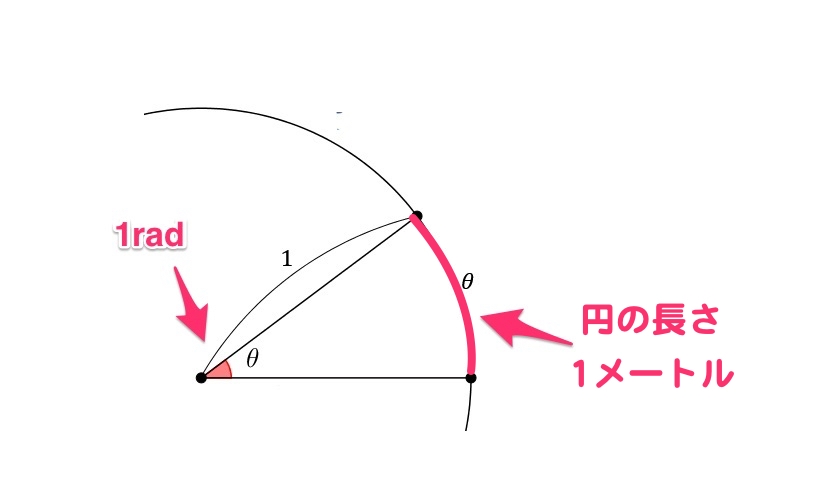
『ラジアン』は、『円の周りの長さ』を重要視しています。

半径が1メートルの円があったとして、
円の周りの長さが1メートルの時の角度を決めちゃおうとなって、

『1ラジアン』と呼ぶことになりました。

• 1rad・・・1ラジアン。
• 円の周りの長さ・・円弧(えんこ)と呼びます。

円の周り(円周)の長さは、

• 円周の長さ = (半径+半径) × 円周率
• 円周の長さ$$ = 2 \pi r $$

ということになっているので、

例えば半径が1メートル、直径2メートルの円周の長さは、

円周の長さ = $$ 2 \pi $$

となります。

(本当は $$ 2rad \pi $$ なのですが、radはカットするようです。)

円周の長さをそのまま角度として扱うのが『ラジアン』なので、

• 360度 = $$ 2 \pi $$ <- これが角度
• 180度 = $$ \pi $$ <- これが角度
• 90度 = $$ \frac{1}{2} \pi $$ <- これが角度

ということになります。

『プログラム』でぴったり『回転』させようと思ったら、この法則を使うというわけですね。

ラジアンをわかりやすく・・度数法をラジアンに変換

実はこの『ラジアン(弧度法)』は、国際単位系の角度の単位になっており、

世界中で一般的な考え方だったりします。

一方で、

という意見も多数あり、確かに、

半径なら180度、直角なら90度というのもわかりやすいので、

度数法を『ラジアン』に変換して使う。

という方法が考え出されました。

度数法を『ラジアン』に変換して使うための計算式はこうなります。

ラジアン$$ = 角度 \times \pi \div 180$$

例えば90度なら、

ラジアン$$ = 90 \times \pi \div 180$$
$$ = \frac{1}{2} \pi$$
になって、

例えば180度なら、

ラジアン$$ = 180 \times \pi \div 180$$
$ = \pi$
になります。

『プログラム』で使う場合には、
度数法→『ラジアン』に変換する場合もあれば、
専用の関数が用意されている『プログラム言語』もあります。

『JavaScript』なら、
最初に角度を指定して、
Math.PI をかけて180度で割ってとしたり、

var $angle = 30;
var $radian = Math.PI * $angle / 180;

『PHP』なら deg2rad関数があり、

『Python』ならmath.degrees関数があったりします。

人にとってわかりやすい角度での指定を、

より正確な値で使うために、『ラジアン』に変換するということですね。

ラジアンとは わかりやすく 度数法とラジアンの変換表

度数と『ラジアン』の主要な角度の変換表をつくってみました。

よく使うのは、

• 45度
• 90度
• 180度
• 360度

の4つかなと思います。

度数（deg)	ラジアン（rad, 弧度）
0	0
30	$$\frac{\pi}{6}$$
45	$$\frac{\pi}{4}$$
60	$$\frac{\pi}{3}$$
90	$$\frac{\pi}{2}$$
120	$$\frac{2}{3}\pi $$
135	$$\frac{3}{4} \pi$$
150	$$\frac{5}{6} \pi$$
180	$$\pi $$
360	$$ 2\pi $$

ラジアンとは わかりやすく 角速度や角周波数

『ラジアン』は、円の周りの長さを表していて、

• 360度 = $$ 2 \pi $$ <- これが角度

という事になっています。

『円周上を動く(円の周りを動く)』という考え方は、

『プログラム』だけに限らず、実は、

• 波
• 電気

など、いろんなところで使われています。

『円周上で動く』速度や周波数は特別に、
『角(かく)』をつけて表します。

• 角速度・・円周上で動く速度
• 角加速度・・円周上で動く加速度
• 角振動数・・円周上で考える振動数
• 角周波数・・円周上で考える周波数

などなど。

関連記事

例えば『波』の場合は、

『円周上を何回回ったか』

というのが大事になってくるので、

『角度』で考えるより、『ラジアン』で考えた方がわかりやすくなってきます。

• 円を1周・・$$ 1 \times 2 \pi = 2\pi $$
• 円を2周・・$$ 2 \times 2 \pi= 4 \pi $$
• 円を3周・・$$ 3 \times 2 \pi= 6 \pi $$
• 円を4周・・$$ 4 \times 2 \pi= 8 \pi $$
• 円を40周・・$$ 40 \times 2 \pi= 80 \pi $$

と聞かれても、なかなかとっさには返せないですが、

『ラジアン』の場合は、

$$ 2 \pi $$を40周なので $$ 80 \pi $$ですな。

っというのがさくっと計算できるようになります。

ラジアンをわかりやすくまとめてみて

キャラクターなり図形なりを動かそうと思うと、

『傾き』だったり『回転』だったりがどうしても必要になってきます。

『度数』で設定することももちろんできるのですが、

より厳密に、ぴったり合わせるためのツールが『ラジアン』かなと思います。

また、『波』や『電気』の分野となると、

1周ではなく何十周も、何百周もすることになるので、

『ラジアン』で表現した方がわかりやすいということにもなりますね。

参考記事
ラジアン（弧度法）の意味と「度」への変換方法

『数学・物理』関係ではこんな記事も読まれています。

1. 【P5.js】初心者向けの動画をリリースしました(プログラミング×数学物理)【Udemy】

2. 【ベクトル】をわかりやすくするコツ〜『ベクトル』はただの数値の組み合わせです(4)【P5.js】

3. プログラムで数学も身につく 一石四鳥なクリエイティブコーディング

4. 【三角関数】の使い方〜わかりやすさ重視でまとめてみた【動画あり】

5. 【ラジアン】とは わかりやすくまとめてみた【初心者向け】

6. 【図解】波の用語や動きをプログラムも交えてまとめてみる【数学&物理】

7. 【微分】とは わかりやすくまとめてみた〜めっちゃすごいわり算【初心者向け】

8. 【シグマ(∑)】計算をわかりやすくまとめてみた【エクセルのsum】【初心者向け】

9. 【極座標 】とは【直交座標 】との違いや変換方法についてまとめてみた

10. 【虚数】【複素数】とは わかりやすくまとめてみた【初心者向け】

11. 【指数】とは わかりやすくまとめてみた【初心者向け】

12. 【対数】とは わかりやすくまとめてみた【初心者向け】

13. 順列・組み合わせ・階乗とは わかりやすくまとめてみた【数学】

14. 【確率(加法定理)】とは わかりやすくまとめてみた【初心者向け】

15. 【ベクトル場】と【速度ベクトル】とは わかりやすく【ドラクエのすべる床】

↓ ここから下は物理関連

1. プログラムで【加速度】をわかりやすくするために実際に動かしてみる(5)【P5.js】

2. 【流体力学】とは 圧力・密度・浮力をまとめてみた【初心者向け】

↓ ここから下はちょいムズカシイ

1. 【ネイピア数】とは わかりやすくまとめてみた【自然対数の底(e)】

2. 【ベクトル解析 勾配(grad)】わかりやすくまとめてみた

3. 【ベクトル解析 発散(div)】わかりやすくまとめてみた

4. 【テイラー展開】をわかりやすくまとめてみた【おすすめ動画あり】

アオキのツイッターアカウント。