『プログラム』でかっこいい映像をつくりたいといろいろググっているうちに、
やけに目にする機会が増えた、『指数(しすう)』と『対数(たいすう)』。
『指数』ってこんなの。
$$2^3 = 2 \times 2 \times 2 = 8$$
グラフはこう。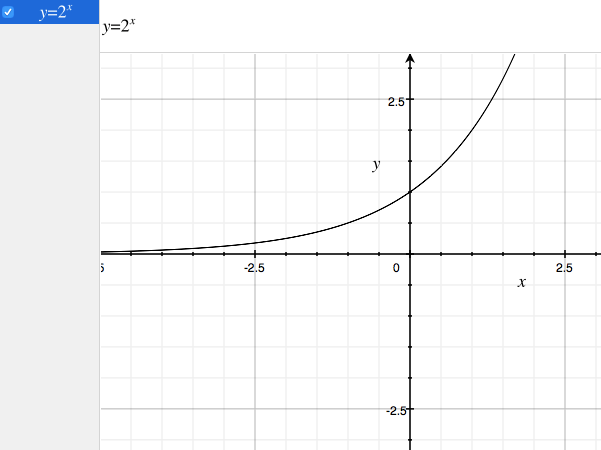
『対数』ってこんなの。
$$\log_{ 2 } 8 = 3$$
グラフはこう(常用対数の場合)。
『指数』と『対数』は掛け算と割り算、表裏一体みたいな関係になっているそうで。
なんて思っていたんですが、
よくよく調べてみると、
- 経済学
- 統計学
- 物理学(熱も流体も)
- 生物学
- 科学
- 情報工学(IT)
- コンピュータグラフィックス
- 日常生活(音、震度、天気、電波、スマホ)
などなど、
実はものすごい範囲で使われている事を知りました。
ということで、できるだけわかりやすくまとめてみることにしました。
『指数』の記事
この記事では『対数』についてまとめています。
対数をわかりやすく 対数の由来
っと思って調べてみると、
1600年代に数学者『ジョン・ネイピア』が考案したそうで、
『logos』(比、神の言葉)とギリシャ語の『arithmos(数)』を合わせた
『logarithms(ロガリズム) 』という造語の略だそうです。
なぜに『対数』を生み出したかというと、
大きい数の計算を簡単にしたかったから。
大航海時代は計算との闘いでもあったのです。
天文学者は直面する天文学的計算を克服する手立てを見つけることができませんでした。
彼らの計算を助けるために、ネイピアはついに新しい計算法を見つけ出す決心をします。
時にネイピア44歳、1594年。
その20年後の1614年、ついに人類は青天の霹靂として「対数」を手にします。〜中略〜
数学者ラプラスをして「対数は天文学者の寿命を倍に延ばした」と言わしめました。
対数をわかりやすく 計算の仕方
『対数』はこう書きます。
$$ \log_{ 2 } 8 = 3$$
- logの右下の小さな値・・『底(てい)』・・この式では2
- 『底』の右の数値・・『真数(しんすう)』・・この式では8
- 『対数(たいすう)』・・この式では3
慣れないうちは、
$$ \log_{ 2 }8 $$ の場合は、
2を何乗したら8になる?
と考えるといいようです。
$$ \log_{ 3 }27 $$の場合。
3を何乗したら27になる?・・ $$3 \times 3 \times 3 $$なので 『対数』は3
$$ \log_{ 10 }1000 $$ の場合。
10を何乗したら1000になる?・・ $$ 10 \times 10\times 10 $$なので 『対数』は3。
と思っちゃうのですが、何度かやってみるうちにちょっとずつ慣れてくるのかなと思います。
対数をわかりやすく 対数法則で計算を簡単に
『対数』にはいくつかの計算法則が存在します。
- $$ \log_{ a}(M \times N) = \log_{ a}M + \log_{ a}N $$
- $$ \log_{ a}\frac{M}{N} = \log_{ a}M – \log_{ a}N $$
- $$ \log_{ a}M^r = r \times \log_{ a}M $$
- $$ \log_{ a}1 = 0, \log_{ a}a = 1$$
※aは正で1でない数。 M,Nを正の数の場合。
よくよく見ると、
- かけ算が足し算に
- わり算が引き算に
- 累乗がかけ算に
変換できるようになっています。
また、
『指数』を『対数』の式に変換する事ができます。
$$ M^k = N $$ の対数をとると、
$$ \log_{ a}M^k = \log_{a}N $$ になる。
これらの法則を使って、
例えば $$ 2^{100} $$の桁数を計算してみます。
$$ N = 2^{100} $$
$$ = \log_{ 10}2^{100} $$
$$ = 100\log_{ 10}2 $$
$$ = 100 \times 0.30103.. $$
$$ N = 30.103 $$
となって、
$$ 2^{100} $$は 『10の30.103乗』
というように計算できるようになります。
参考記事:対数とは何なのかとその公式・メリットについて。対数をとるとはどういう意味か?
対数をわかりやすく 常用対数と自然対数
- logの右下の小さな値・・『底(てい)』
といいますが、
『対数』は大きく2パターンの『底(てい)』に分かれるようです。
- 常用対数・・底が10
- 自然対数・・底がネイピア数(e)
対数をわかりやすく 常用対数とは
『常用対数(じょうようたいすう)』は、『底(てい)』が10の『対数』の事です。
『常用対数表』なる表もあるようです。
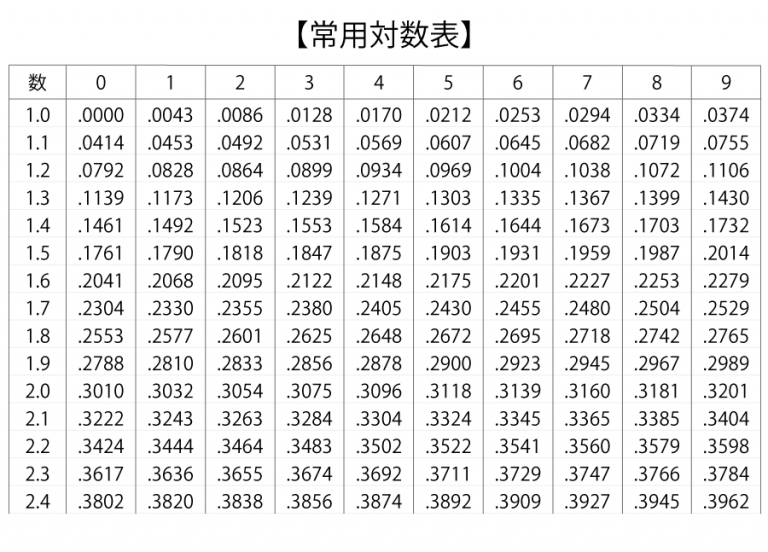
『常用対数表』の見方はこう。
- 左端の数字・・少数第一位までの数字
- 上端の数字・・少数第二位の数字
例えば $$ \log_{ 10 }1.83 $$なら
- 左端・・1.8
- 上端・・3
の交わる箇所になるので、
$$ \log_{ 10 }1.83 = 0.2625 $$
になります。
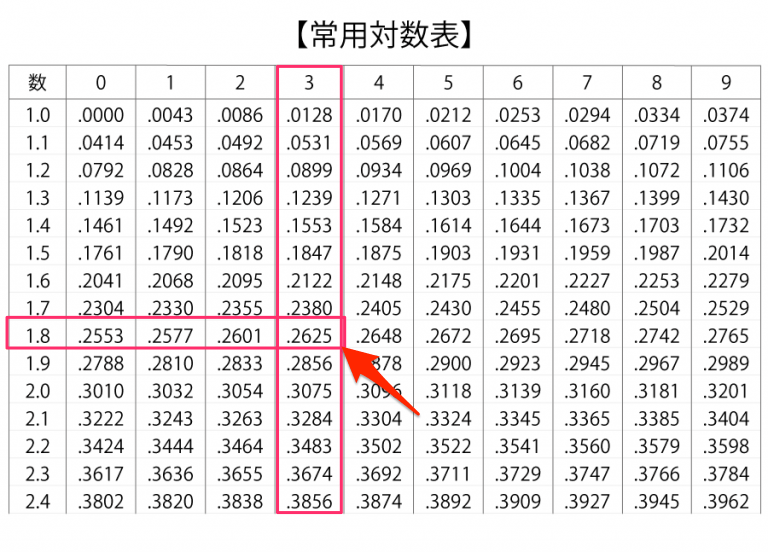
『常用対数』をグラフにするとこんな感じになります。
対数をわかりやすく 自然対数とは
一方、『自然定数(しぜんたいすう)』はというと、
『底』が『ネイピア数(e)』になる『対数』の事です。
となったので調べてみるとどうやら、
- 1/nの確率で当たるくじ
- 2つのトランプのカードが一致する確率
- 秘書問題(応募者が採用できる確率)
- 正規分布やポアソン分布
- 放射性物質の半減期
- 化学反応における物質濃度の半減期
- お湯の冷却温度の変化
- マルサスモデル(生物の個体数などの増加や減少)
- 対数螺旋(カタツムリ、牛のツノ、台風など)
などなど、
たくさんの分野で『ネイピア数』が使われているようです。
参考記事
『自然対数』のグラフはこうなります。
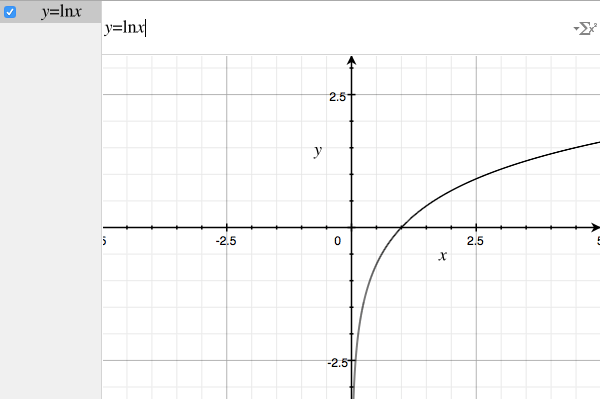
対数をわかりやすく 人間の感覚は対数的
普段の生活ではなかなかお目にかかれない『対数』ですが、
実は身近なところでいろいろと使われています。
- 地震の大きさ・・震度
- 音の大きさ・・デシベル(db)
- 星の明るさ・・等星
- 酸性アルカリ性・・Ph(ペーハー)
- 音階・・(ド、レ、ミ)
などなど。
対数をわかりやすくまとめてみて
『指数』も『対数』も、
『シェーダ』や『統計学』や『物理・化学』の分野ではそれはもう必修のようで、
これからちょくちょく見直しつつ加筆しつつ、役立つページにしていきたいと思います。
『数学・物理』関係ではこんな記事も読まれています。
1. 【P5.js】初心者向けの動画をリリースしました(プログラミング×数学物理)【Udemy】2. 【ベクトル】をわかりやすくするコツ〜『ベクトル』はただの数値の組み合わせです(4)【P5.js】
3. プログラムで数学も身につく 一石四鳥なクリエイティブコーディング
4. 【三角関数】の使い方〜わかりやすさ重視でまとめてみた【動画あり】
5. 【ラジアン】とは わかりやすくまとめてみた【初心者向け】
6. 【図解】波の用語や動きをプログラムも交えてまとめてみる【数学&物理】
7. 【微分】とは わかりやすくまとめてみた〜めっちゃすごいわり算【初心者向け】
8. 【シグマ(∑)】計算をわかりやすくまとめてみた【エクセルのsum】【初心者向け】
9. 【極座標 】とは【直交座標 】との違いや変換方法についてまとめてみた
10. 【虚数】【複素数】とは わかりやすくまとめてみた【初心者向け】
11. 【指数】とは わかりやすくまとめてみた【初心者向け】
12. 【対数】とは わかりやすくまとめてみた【初心者向け】
13. 順列・組み合わせ・階乗とは わかりやすくまとめてみた【数学】
14. 【確率(加法定理)】とは わかりやすくまとめてみた【初心者向け】
15. 【ベクトル場】と【速度ベクトル】とは わかりやすく【ドラクエのすべる床】
↓ ここから下は物理関連
1. プログラムで【加速度】をわかりやすくするために実際に動かしてみる(5)【P5.js】
2. 【流体力学】とは 圧力・密度・浮力をまとめてみた【初心者向け】
↓ ここから下はちょいムズカシイ
1. 【ネイピア数】とは わかりやすくまとめてみた【自然対数の底(e)】
2. 【ベクトル解析 勾配(grad)】わかりやすくまとめてみた
3. 【ベクトル解析 発散(div)】わかりやすくまとめてみた
4. 【テイラー展開】をわかりやすくまとめてみた【おすすめ動画あり】
アオキのツイッターアカウント。

















この記事へのコメントはありません。