『3Dプログラミング』で『回転』をさせたいなとその方法を探るうちに、

よく見かけるようになった、『虚数(きょすう)』と『複素数(ふくそすう)』。

ということで、『虚数』と『複素数』について、まるっとまとめてみることにしました。

虚数とは わかりやすく 由来と目的

そもそも『虚数(きょすう)』という名前がとっつきにくかったので、

英語だとどう書いてあるか調べてみると、

『imaginary number(イマジナリーナンバー)(想像上の数)』という意味だそうです。

実際には存在しない数字をなぜにつくったのかというと、

• その方が計算がしやすくなる
• その方が回転しやすくなる
• その方が周期性のある(繰り返しのある)計算が楽になる

といった目的があったそうで、

• 波
• 音
• 電磁波
• 交流電流
• 3Dプログラミング

などの分野でよく使われているようで。

歴史的には、

• 1500年代に『ジェロラモ・カルダーノ』が発見して
• 1637年にデカルトが初めて『虚数』という言葉を使って
• 『レオンハルト・オイラー』や『カール・フリードリヒ・ガウス』を経て
• 1843年に『ウィリアム・ローワン・ハミルトン』が四元数に拡張

といった流れがあるそうです。

虚数とは わかりやすく 虚数で回転させてみる

現実世界に存在しない数が『虚数(imaginary number)』なんですが、

具体的にいうと、

2乗して -1 になる数字のことだそうです。

$i^2 = -1$
$i = \pm\sqrt-1$

• 実際に存在する数・・『実数(real number)(リアルナンバー)』
• 想像上の数・・『虚数(imaginary number)(イマジナリーナンバー)』

と区別して、平面に置いてみます。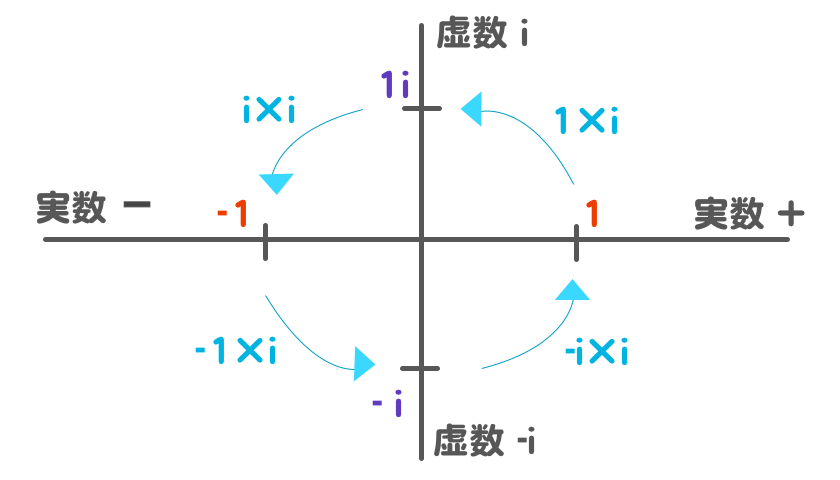

• 1 に i をかける・・1i になる
• 1iにiをかける・・ i × i で -1 になる
• -1にiをかける・・-i になる
• -iにiをかける・・-i × i で 1 になる

と、ぐるっとまわるように描くことができます。

虚数とは わかりやすく 複素数とは

• 実際に存在する数・・『実数(real number)(リアルナンバー)』
• 想像上の数・・『虚数(imaginary number)(イマジナリーナンバー)』

として、

『実数』+『虚数』の組み合わせを、
『複素数(ふくそすう)』というそうです。

• 『複素数』・・英語で『complex number(コンプレックスナンバー)』
• complex・・日本語だと複合とか混合とか

こちらも『実数』と『虚数』を組み合わせて平面をつくってみると、

『複素数』(3+2i) の場合はこうなります。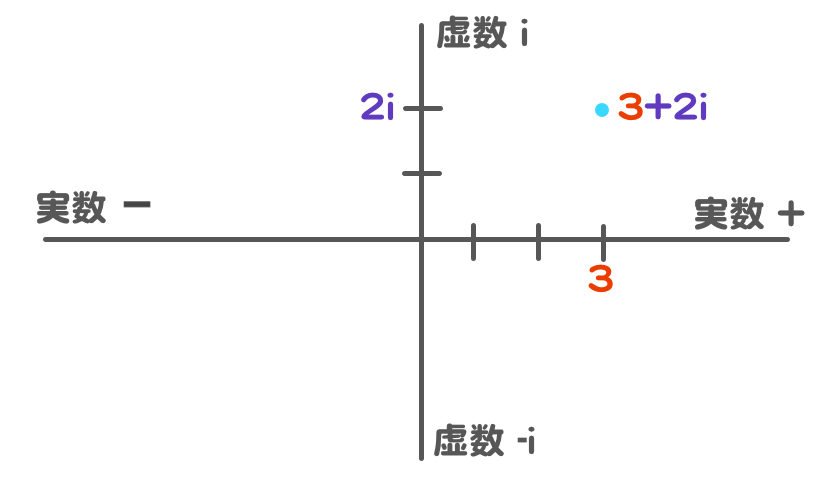

虚数とは わかりやすく オイラーの公式

『虚数(imaginary number』を一躍有名にしたのが、

天才数学者『レオンハルト・オイラー』。

『レオンハルト・オイラー』がつくった等式・公式がこちら。

■オイラーの等式

$$e^{i\pi} = -1$$

■オイラーの公式
$$e^{i\pi} = \cos\theta +i\sin\theta$$

• 『虚数 i』
• 『円周率 π』
• 『ネイピア数 e』

の3つの要素がシンプルな形で組み合わさっていて、

『数学史上もっとも素晴らしい公式』という人もいるようです。

物理学者の『リチャード・ファインマン』は、
この公式を評して
「我々の至宝」かつ「すべての数学のなかでもっとも素晴らしい公式」だと述べている。

参考：Wikipedia オイラーの公式

証明は、『テイラー展開(マクローリン展開)』を使うのですが、
ちょっと長くなるので他記事を参照いただきたく。

オイラーの公式とは何か？オイラーの等式の求め方の流れを紹介【我々の至宝と評された公式】

『ネイピア数』の参考記事

『ラジアン』の参考記事

『テイラー展開(マクローリン展開)』の参考記事

虚数とは わかりやすく 四元数(クォータニオン)

『3Dプログラミング』をやっていると、

物体を『回転』させる方法として、

『クォータニオン』を使う、なんて事がよく書かれています。

• クォータニオン(英語でQuaternion。日本語で四元数(しげんすう)

よくよくググってみるとどうやら『虚数』を『拡張』した方法だそうで。

と言ったかどうかはさておいて、

角度と3つの虚数を組み合わせることで、

3D空間の姿勢なども制御できるようになるようです。

クォータニオン (Quaternion) を総整理！ ～ 三次元物体の回転と姿勢を鮮やかに扱う ～

クォータニオン(四元数)

虚数とは わかりやすくまとめてみて

元々は、『クォータニオン』から先に知って、
少しずつ深掘りして、ようやく記事がかけるようになりました。

『オイラーの公式』などは『物理学』では必須のようで、

まだまだ使いこなせていない感があるので、

何度か繰り返してものにしていきたいところです。

『数学・物理』関係ではこんな記事も読まれています。

1. 【P5.js】初心者向けの動画をリリースしました(プログラミング×数学物理)【Udemy】

2. 【ベクトル】をわかりやすくするコツ〜『ベクトル』はただの数値の組み合わせです(4)【P5.js】

3. プログラムで数学も身につく 一石四鳥なクリエイティブコーディング

4. 【三角関数】の使い方〜わかりやすさ重視でまとめてみた【動画あり】

5. 【ラジアン】とは わかりやすくまとめてみた【初心者向け】

6. 【図解】波の用語や動きをプログラムも交えてまとめてみる【数学&物理】

7. 【微分】とは わかりやすくまとめてみた〜めっちゃすごいわり算【初心者向け】

8. 【シグマ(∑)】計算をわかりやすくまとめてみた【エクセルのsum】【初心者向け】

9. 【極座標 】とは【直交座標 】との違いや変換方法についてまとめてみた

10. 【虚数】【複素数】とは わかりやすくまとめてみた【初心者向け】

11. 【指数】とは わかりやすくまとめてみた【初心者向け】

12. 【対数】とは わかりやすくまとめてみた【初心者向け】

13. 順列・組み合わせ・階乗とは わかりやすくまとめてみた【数学】

14. 【確率(加法定理)】とは わかりやすくまとめてみた【初心者向け】

15. 【ベクトル場】と【速度ベクトル】とは わかりやすく【ドラクエのすべる床】

↓ ここから下は物理関連

1. プログラムで【加速度】をわかりやすくするために実際に動かしてみる(5)【P5.js】

2. 【流体力学】とは 圧力・密度・浮力をまとめてみた【初心者向け】

↓ ここから下はちょいムズカシイ

1. 【ネイピア数】とは わかりやすくまとめてみた【自然対数の底(e)】

2. 【ベクトル解析 勾配(grad)】わかりやすくまとめてみた

3. 【ベクトル解析 発散(div)】わかりやすくまとめてみた

4. 【テイラー展開】をわかりやすくまとめてみた【おすすめ動画あり】

アオキのツイッターアカウント。