というニーズに応える方法として生み出されたのが『テイラー展開』。

『ブルック・テイラー』(1685-1731) が導入したと言われています。

『テイラー展開』の特徴はこれら。

・複雑な関数を『多項式』で表せる
・ある1点の情報から近所(近接)の事を知る事ができる

ということで、まずは『単項式(たんこうしき)』と『多項式(たこうしき)』の違いからまとめてみます。

テイラー展開をわかりやすく まずは単項式と多項式

まずは『単項式(たんこうしき)』から。

『単項式』は掛け算だけでできています。

$$ 2y= 2 \times y $$
$$ -50y= -50 \times y $$
$$ 3abc= 3 \times a \times b \times c $$

掛け算の「×」は省略できて、くっつけられるので、
『2y』『-50y』『3abc』はそれぞれ1つの『項(こう)』ということになります。

続いて『多項式』。
$$ 2a + b = 2 \times a + b $$
$$ 2a^2 – 3b^2 = 2 \times a \times a + ( -3 \times b \times b) $$
$$ 10a^2 + b = 10 \times a \times a + b $$

『多項式』は「+」や「-」が含まれていて、
いくつかの『項(こう)』をくっつけた式になっています。

テイラー展開をわかりやすく マクローリン展開とは

『テイラー展開』は、
ある1点の情報から近所の事を知るというのが大きい特徴なのですが、

ある1点が 0 (原点まわり)の場合は特別に、
『マクローリン展開』とも呼ぶそうです。

• 『コリン・マクローリン』(1698-1746) スコットランドの数学者。

18世紀に『ブルック・テイラー』さんが提唱した時に、
『マクローリン展開』と言っていたとかいないとか。

テイラー展開をわかりやすく ある1点から近所の事を知るって？

教育系Youtuber『ヨビノリたくみ』さんの動画を参考にまとめてみました。

お題で上がっていたのは、

『指数関数』$$ f(x) = e^x $$ を

$$ x = 0 $$まわりで『テイラー展開』するという内容で。

$$ e $$ は『ネイピア数』と言って、
グラフにするとこんな形にぐいーんと伸びていく形になります。

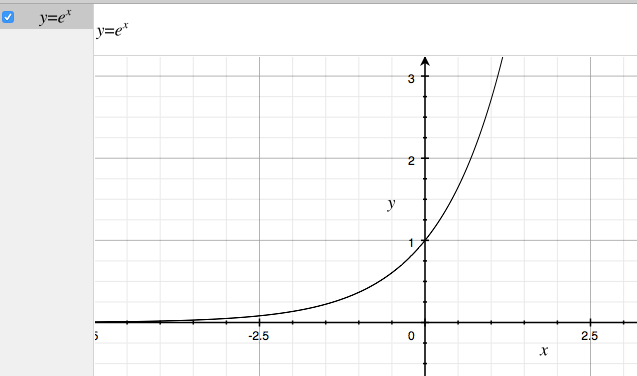
『ネイピア数』の参考記事

テイラー展開をわかりやすく ステップ1 1次関数を見つける

まずは、$$ x = 0 $$ の近くで、$$ f(x) = e^x $$ っぽい『1次関数』を見つけます。

• 1つめの条件・・xに0を代入したら1になる。(0次近似(ゼロジキンジ)といいます。)

$$ f(0) = 1 $$

• 2つめの条件・・『微分』して0を入れても同じ値になってほしい。(1次近似(イチジキンジ))

$$ f'(0) = 1 $$

微分の参考記事

2つを満たす1次関数はこれ。
$$ f(x) = 1 + x $$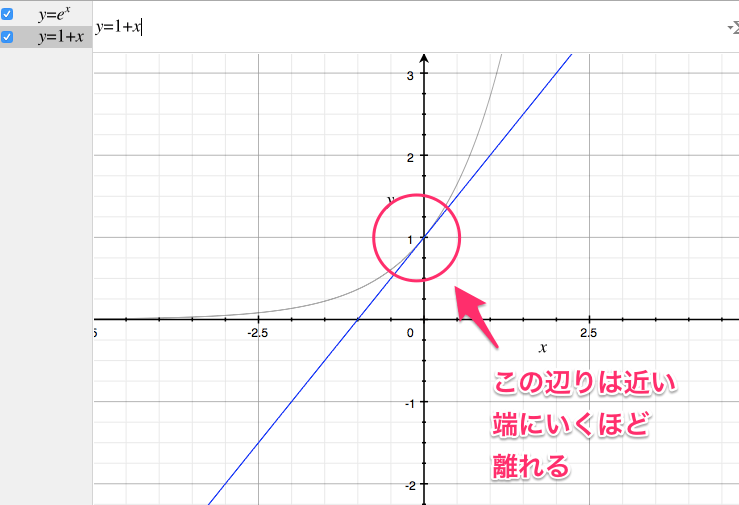

でも『1次関数』は直線なので、曲がってる箇所は寄せれません。

テイラー展開をわかりやすく ステップ 2次関数を見つける

『2次関数』ならぐいっと曲げて表現できるので、

$$ x = 0 $$ の近くで、$$ f(x) = e^x $$ っぽい『2次関数』を見つけます。

• 1つめの条件・・xに0を代入したら1になる。(0次近似)

$$ f(0) = 1 $$

• 2つめの条件・・『微分』して0を入れても同じ値になる。(1次近似)

$$ f'(0) = 1 $$

• 3つめの条件・・2次関数なので『2階微分』して0を入れても同じ値になってほしい。(2次近似)

$$ f”(0) = 1 $$

3つの条件を満たす式はこれ。

$$ f(x) = 1+x+ \frac{1}{2}x^2 $$

グラフにのせてみると・・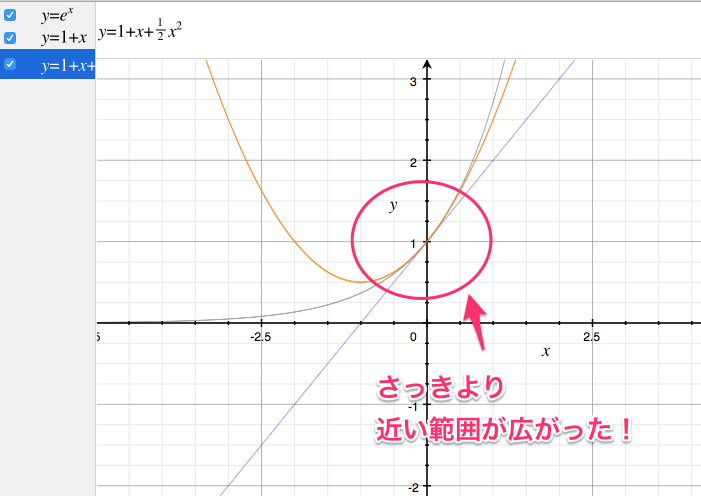

この要領で、もっと近づけるためには、

• 3次関数
• 4次関数
• 5次関数
• 6次関数
• n次関数
• ・・・

と次元をあげて、無限に繰り返せば、グラフにぴったり寄せることができるということになるようです。

テイラー展開をわかりやすく 一般のテイラー展開も同じ要領で

テイラー展開の式は以下。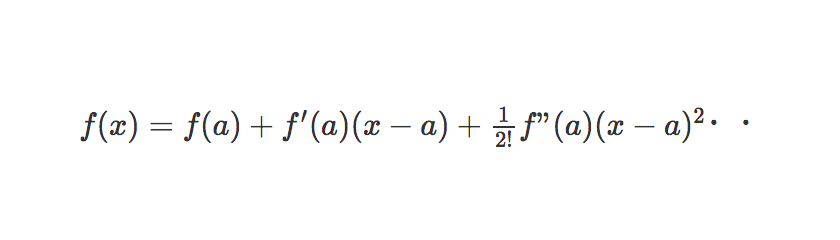

xにaを入れると、f(a)だけ残って、後ろは全部0になります。(0次近似)
f(a) = a (後ろは全部0)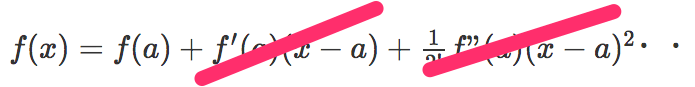

『1階微分』にaを入れてf'(a)にすると、
定数が消えて、f'(a)だけ残って、後ろは全部消えます。(1次近似)

『2階微分』にaを入れてf”(a)にすると、f”(a)だけ残ることに。(2次近似)

無限にやっていくとイコールになります。

テイラー展開をわかりやすく sinxでも試してみる

参考動画の最後に、

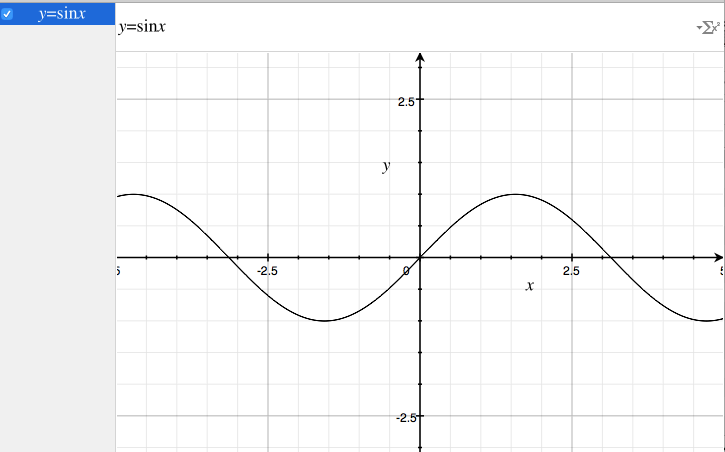
$$ y = sinx $$

を『テイラー展開』した時のグラフが載っていたのでやってみる事にしました。

参考記事

$$ sinx $$を『テイラー展開』した時の式はこう。

$$ y = x – \frac{1}{3!}x^3 + \frac{1}{5!}x^5 $$ ・・・

1つずつグラフに載せてみると・・

0次近似。$$ y = x $$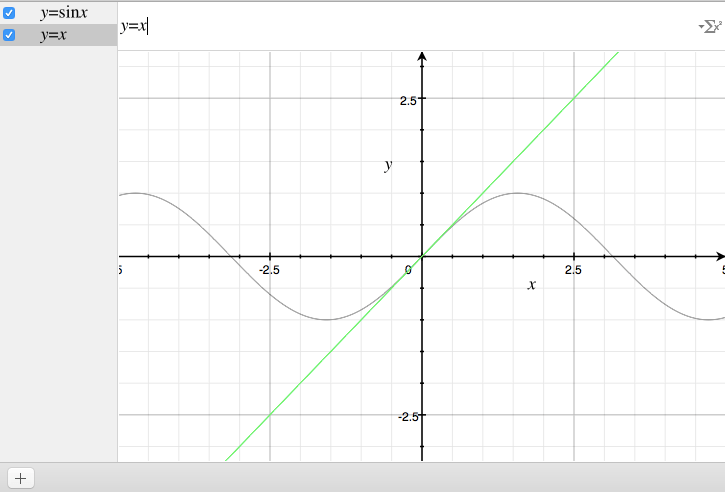

1次近似。$$ y = x – \frac{1}{3!}x^3 $$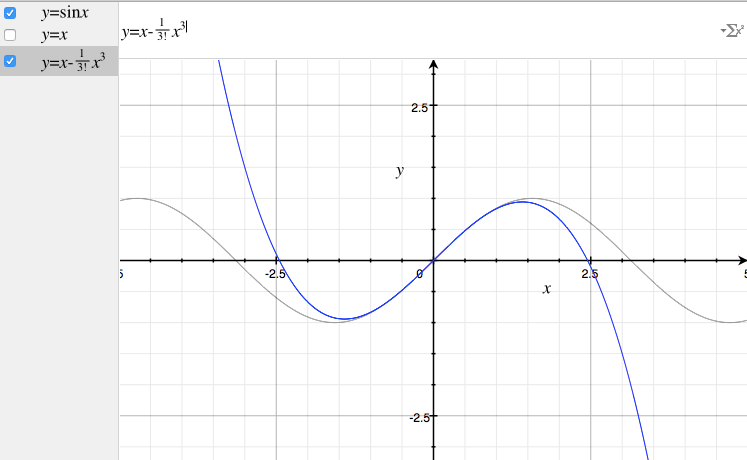

2次近似。$$ y = x – \frac{1}{3!}x^3 + \frac{1}{5!}x^5 $$

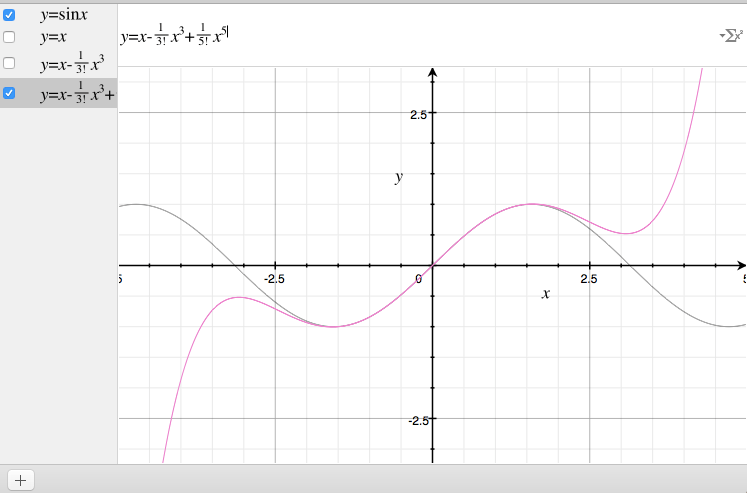
3次近似。$$ y = x – \frac{1}{3!}x^3 + \frac{1}{5!}x^5 – \frac{1}{7!}x^7 $$

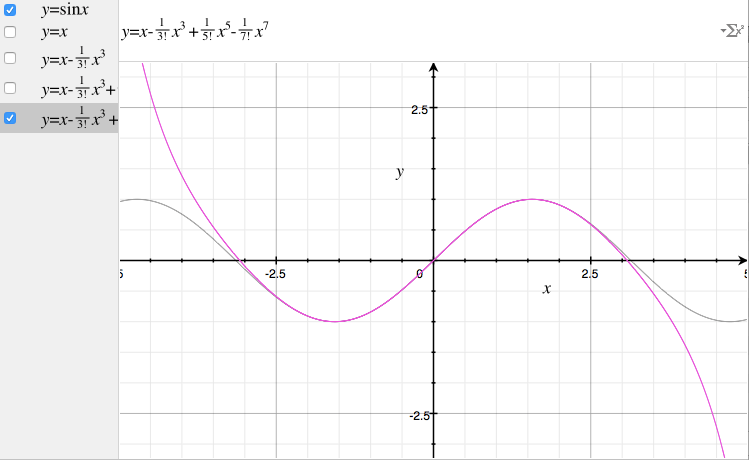
4次近似。$$ y = x – \frac{1}{3!}x^3 + \frac{1}{5!}x^5 – \frac{1}{7!}x^7 + \frac{1}{9!}x^9 $$

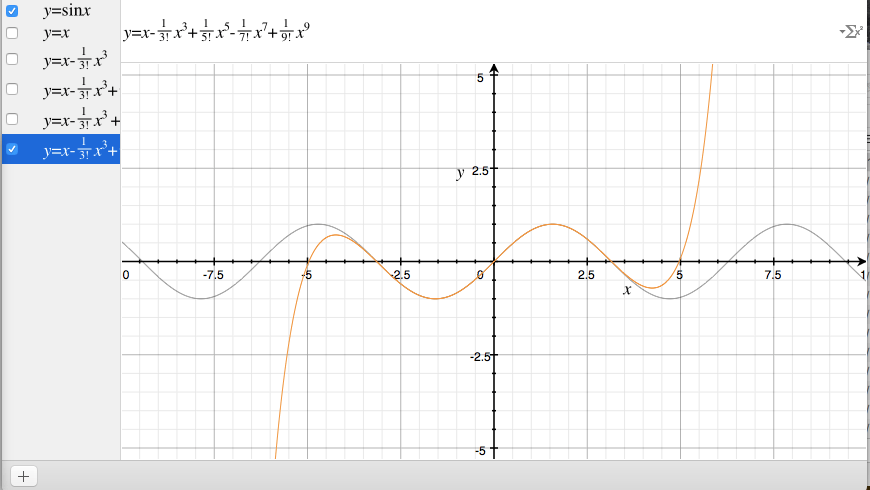
他にも『テイラー展開』できる式はたくさんあって、ウィキペディアにまるっとまとまっています。

• 指数関数
• 自然対数
• 幾何級数
• 二項定理
• 三角関数
• 双曲線関数
• ランベルトのW関数

などなど。

無限に繰り返すので『シグマ($$ \sum$$ )』で表現されていますが、考え方は同じです。

テイラー展開 | Wikipedia

テイラー展開をわかりやすくまとめてみて

複雑な式をできるだけ簡単に表現しようとした『テイラー展開』。

式の丸暗記は流石にしんどいので、

『テイラー展開』の目的、やりたい事をぼんやりと知っておきつつ、

・複雑な関数を『多項式』で表せる
・ある1点の情報から近所の事を知ることができる

複雑な式も簡単に解きほぐせるという事を知っておくと、
よりややこしい式も使いこなせるようになるようです。

　

『数学・物理』関係ではこんな記事も読まれています。

1. 【P5.js】初心者向けの動画をリリースしました(プログラミング×数学物理)【Udemy】

2. 【ベクトル】をわかりやすくするコツ〜『ベクトル』はただの数値の組み合わせです(4)【P5.js】

3. プログラムで数学も身につく 一石四鳥なクリエイティブコーディング

4. 【三角関数】の使い方〜わかりやすさ重視でまとめてみた【動画あり】

5. 【ラジアン】とは わかりやすくまとめてみた【初心者向け】

6. 【図解】波の用語や動きをプログラムも交えてまとめてみる【数学&物理】

7. 【微分】とは わかりやすくまとめてみた〜めっちゃすごいわり算【初心者向け】

8. 【シグマ(∑)】計算をわかりやすくまとめてみた【エクセルのsum】【初心者向け】

9. 【極座標 】とは【直交座標 】との違いや変換方法についてまとめてみた

10. 【虚数】【複素数】とは わかりやすくまとめてみた【初心者向け】

11. 【指数】とは わかりやすくまとめてみた【初心者向け】

12. 【対数】とは わかりやすくまとめてみた【初心者向け】

13. 順列・組み合わせ・階乗とは わかりやすくまとめてみた【数学】

14. 【確率(加法定理)】とは わかりやすくまとめてみた【初心者向け】

15. 【ベクトル場】と【速度ベクトル】とは わかりやすく【ドラクエのすべる床】

↓ ここから下は物理関連

1. プログラムで【加速度】をわかりやすくするために実際に動かしてみる(5)【P5.js】

2. 【流体力学】とは 圧力・密度・浮力をまとめてみた【初心者向け】

↓ ここから下はちょいムズカシイ

1. 【ネイピア数】とは わかりやすくまとめてみた【自然対数の底(e)】

2. 【ベクトル解析 勾配(grad)】わかりやすくまとめてみた

3. 【ベクトル解析 発散(div)】わかりやすくまとめてみた

4. 【テイラー展開】をわかりやすくまとめてみた【おすすめ動画あり】

アオキのツイッターアカウント。