先日とあるサイトを見ていたらとてもかっこいい映像を見つけました。
『GLSL』というプログラム言語で見事なカミナリの映像をつくっています。
もしやと思いコードをざっと見ると、
思った通り、『波』の組み合わせがあって。
ということで今回は、
『波』の用語を整理しつつ、
『波』をプログラミングで操れるようになるための土台固めをするつもりで
記事を書いてみたいと思います。
『波』の用語をわかりやすく 周期関数とは
流れるプールや海にいって、プカプカ浮かぶと実感できるのですが、
1回きりの動きではなく、
何度も何度も上がったり下がったりを繰り返すのが『波』の特徴かなと思います。
何度も何度も繰り返すので『周期的(しゅうきてき)』といって、
『周期関数(しゅうきかんすう)』という表現もあるようです。
『波』の用語をわかりやすく 空間的か時間的か
『波』に関する記事やら本やらを見ていると、
どうやら『波』には大きく2つのタイプがあることがわかりました。
- 空間的にとらえる波
- 時間的にとらえる波
の2種類です。
波の用語 空間的にとらえる y-xグラフ
空間的というのは、
プールにボールを投げいれて、
小さな『水波』がふわーっと広がるのを写真でとったような『波』のことで、
『y-xグラフ』で表します。
- 『y-xグラフ』・・ある時刻での波全体の形を表すグラフ。
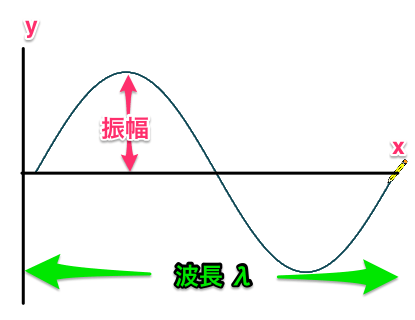
xは位置を表します。
『y-xグラフ』の用語は以下。
- 『振幅(しんぷく) (A)』・・波の幅
- 『波長(はちょう)』・・波の1つのかたまり
- 『λ(ラムダ)』・・『波長(はちょう)』を表すギリシャ記号
『振幅(しんぷく)』は文字通り、波の幅という意味。
英語だと『Amplitude』というなにやら難しい英語になり、大文字『A』で表す場合もあります。
『波長(はちょう)』も文字通り、波の長さ。
『波長』は英語で『wave length(ウェーブレングス)』で、そのままの意訳になります。
『波』は上がったり下がったりを繰り返すので、
上がって下がって戻るまでを1つのかたまりとして見ます。
で、『波長』の単位が『λ(ラムダ)』。
と思い由来をググってみると、
どうやら英語で長さを表す『Length(レングス)』からきてるとかきてないとか。
一見なんじゃこりゃな記号ですが、
波には『幅』と『長さ』の2つがある。
というのがわかればまずはいいのかなと。
波の用語 時間的にとらえる y-tグラフ
続いて、時間的にとらえる『波』。
例えばラジオ、地震、音楽、心臓の鼓動など、
目には見えないし、
波とは思えないものも、
時間を横軸にして記録していくと、『波』のグラフが現れてきます。
『心電図』などですね。
横軸に時間をとるので『y-t』グラフになります。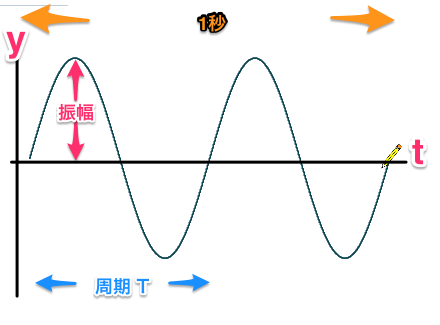
- 『y-tグラフ』・・ある1点での振動の時間変化を表すグラフ。
用語は以下。
- 『振幅(しんぷく)』・・波の幅
- 『周期(しゅうき)(T)』・・波のカタマリ
- 『周波数(振動数) (f)』・・1秒間に振動した回数。単位はHz(ヘルツ)
- 『角周波数(角振動数) (ω)』・・三角関数とセット。説明は後ほど。
『振幅』は『y-x』グラフと同じで波の幅。
『周期』は、1回振動するのにかかる時間で、
例えば1秒間に2回振動するなら、
0.5秒で1回振動するということになるので、
『周期』は0.5秒、になります。
表記は『T』になります。
続いて『周波数(しゅうはすう)』。
『周波数』は英語で『frequency (フレクエンシー)(頻発、なんども起こるという意味)』になり、
頭文字をとって『f』で表したりします。
『周波数』の単位はHz(ヘルツ)。
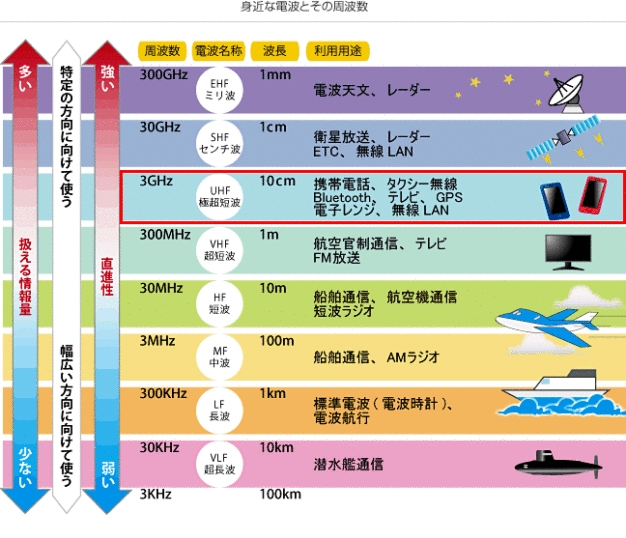
- ラジオの電波
- 携帯電話で使っている電波
- Wifiで使っている電波
などなど、目には見えないけれど、普段の生活でいろんな電波が飛び交っています。
- 1秒間に100回 振動すれば 100Hz で、
- 1秒間に 1,000回振動すれば1KHz (1キロヘルツ)。
- 1秒間に 1,000,000回振動すれば1MHz (1メガヘルツ)。
携帯で使う周波数に800MHzがありますが、
800MHzの場合、1秒間に800,000,000回振動しているという・・・
波の用語をわかりやすく 角周波数(角振動数)
実は『波』は、『三角関数』が深く関わっています。
『三角関数』はこんな動きをします。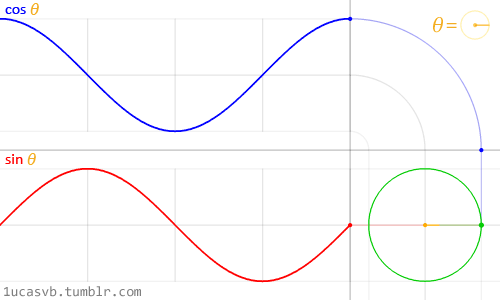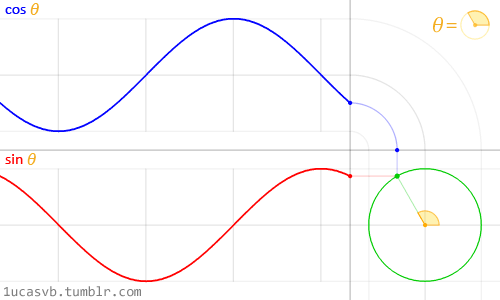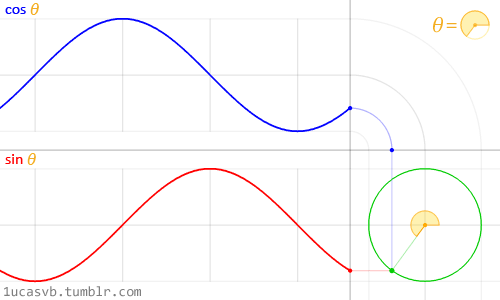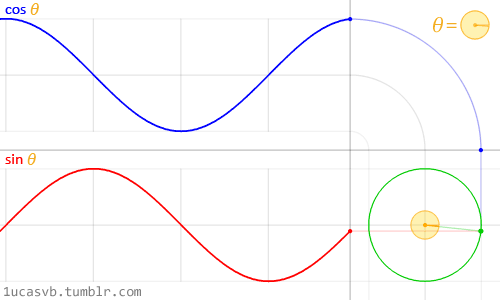
なんでこんな動きするの?って思ったら
こちらの記事を参考にしてみてください。
参考記事
この図のように、
同じスピードで角度が変わっている場合は、
『周波数』を『角度』で表す事もできるようです。
『周波数』を『角度(ラジアン)』で表したものを、
『角周波数(かくしゅうはすう)』または『角振動数(かくしんどうすう)』といいます。
参考記事
『角周波数』は英語で『angular frequency(アンギュラーフレクエンシー)』なのですが、
なぜか、
『角周波数(かくしゅうはすう)』は『ω(オメガ)』で表します。
と由来をググってみたけれどパッとは解説見つからず。
『角周波数 オメガ(ω)』の単位は 『rad/s (ラジアン/秒)』になり、
1秒間の回転角を表します。
- ω = 1 なら、 1秒間に2π 動く(1周する)
- ω = 2 なら、 1秒間に4π 動く (2周する)
- ω = 0.5 なら、 1秒間にπ 動く (半周する)
という具合になります。
波の用語 振幅と角周波数をプログラミングで試してみる
『プログラミング』で波を表現しようとすると、
『振幅』と『角周波数』が必要になってきます。
『振幅』は英語(Amplitude)の頭文字をとって『A』なのですが、
円で考えると『半径』とぴったり一緒になるので、
『半径』の英語(radius)の頭文字『r』で表す場合もあるようです。
- 振幅・・半径なのでr (radiusの略)
- 角周波数・・ω (オメガ)
$$ y=rsinωx $$ という式で、それぞれ数字が入ってきます。
『スクラッチ』でいくつかのパターンを試してみました。
- 振幅(r)が100、角周波数(ω)が1のグラフ・・100sint (tは秒を表す)

- 振幅(r)が150、角周波数(ω)が1のグラフ・・150sint
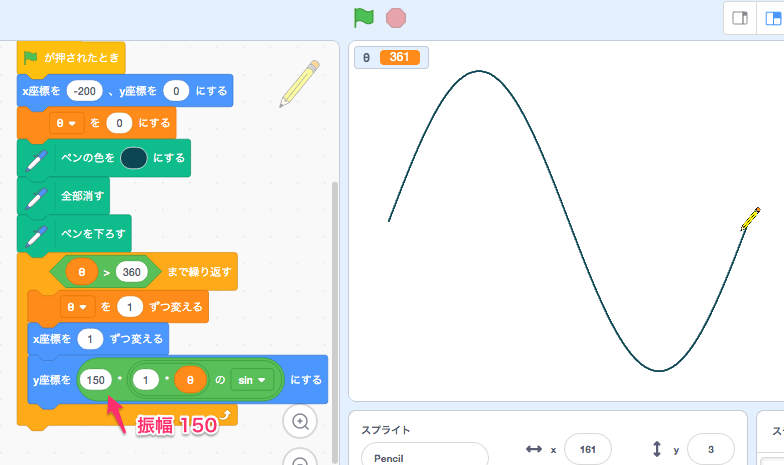
先ほどのグラフより上下に幅が広がっています。
- 振幅(r)が100、角周波数(ω)が2のグラフ・・100sin2t
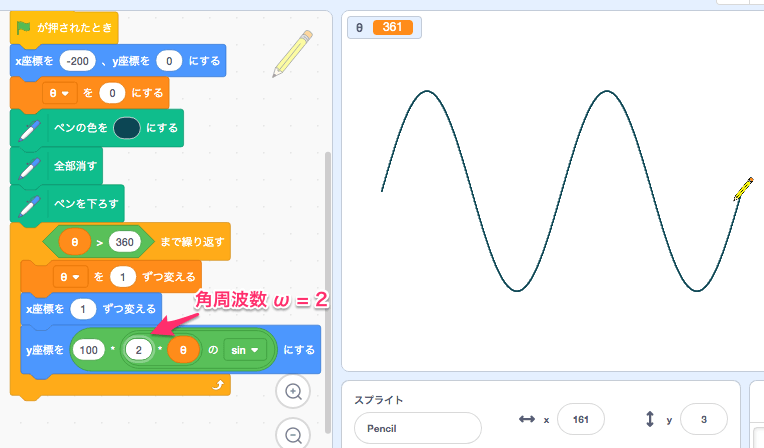
角周波数を2にすると、2 × 2π で 2周分動きます。
- 振幅(r)が100、角周波数(ω)が5のグラフ・・100sin5t
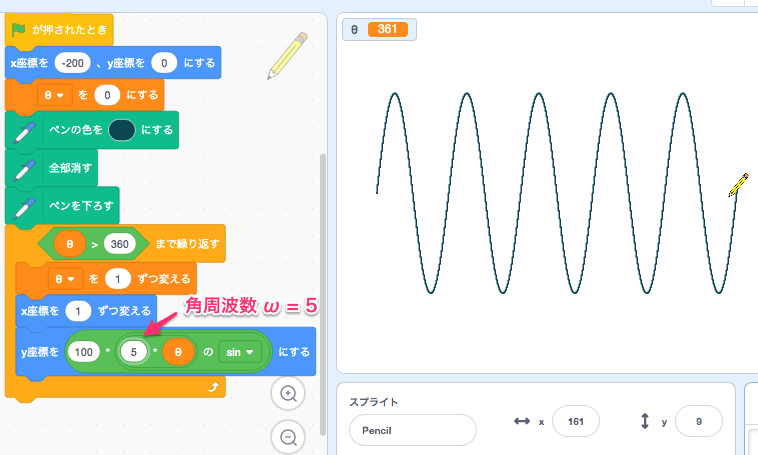
角周波数を5にすると、5 × 2π で 5周分動きます。
波の用語や動きのまとめ
わかりやすさ重視のため、いろんな公式を省いていますので、
しっかりした公式や解説は下記資料を参照いただければと思います。
参考記事
円運動
波動の復習・・残念ながらリンク切れ・・
波としての三角関数
『波』の用語はいろいろあってややこしいものの、
何度も何度も繰り返すという性質を頭に入れつつ、
うまい具合に『プログラミング』にも活かしていけたらなと思います。
実のところ、
ライデインをつくるためにはこれだけの知識では不十分なので、
もうちょい記事を増やしながらレベルアップしていくことにします。
『数学・物理』関係ではこんな記事も読まれています。
1. 【P5.js】初心者向けの動画をリリースしました(プログラミング×数学物理)【Udemy】2. 【ベクトル】をわかりやすくするコツ〜『ベクトル』はただの数値の組み合わせです(4)【P5.js】
3. プログラムで数学も身につく 一石四鳥なクリエイティブコーディング
4. 【三角関数】の使い方〜わかりやすさ重視でまとめてみた【動画あり】
5. 【ラジアン】とは わかりやすくまとめてみた【初心者向け】
6. 【図解】波の用語や動きをプログラムも交えてまとめてみる【数学&物理】
7. 【微分】とは わかりやすくまとめてみた〜めっちゃすごいわり算【初心者向け】
8. 【シグマ(∑)】計算をわかりやすくまとめてみた【エクセルのsum】【初心者向け】
9. 【極座標 】とは【直交座標 】との違いや変換方法についてまとめてみた
10. 【虚数】【複素数】とは わかりやすくまとめてみた【初心者向け】
11. 【指数】とは わかりやすくまとめてみた【初心者向け】
12. 【対数】とは わかりやすくまとめてみた【初心者向け】
13. 順列・組み合わせ・階乗とは わかりやすくまとめてみた【数学】
14. 【確率(加法定理)】とは わかりやすくまとめてみた【初心者向け】
15. 【ベクトル場】と【速度ベクトル】とは わかりやすく【ドラクエのすべる床】
↓ ここから下は物理関連
1. プログラムで【加速度】をわかりやすくするために実際に動かしてみる(5)【P5.js】
2. 【流体力学】とは 圧力・密度・浮力をまとめてみた【初心者向け】
↓ ここから下はちょいムズカシイ
1. 【ネイピア数】とは わかりやすくまとめてみた【自然対数の底(e)】
2. 【ベクトル解析 勾配(grad)】わかりやすくまとめてみた
3. 【ベクトル解析 発散(div)】わかりやすくまとめてみた
4. 【テイラー展開】をわかりやすくまとめてみた【おすすめ動画あり】
アオキのツイッターアカウント。

















この記事へのコメントはありません。