2020/6/9 追記
極座標も扱ったプログラミング講座をリリースしました。
『座標』と言ったらほとんどの人が、
っと思いがちで、
確かに『スクラッチ』でも縦横でつくるようになっているんですが。
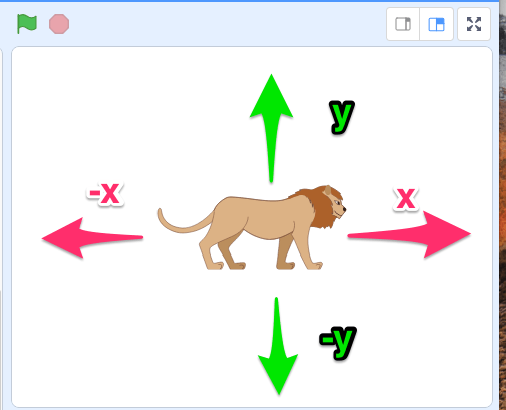
実は『座標』は、縦と横の線だけではなくて、
『距離』と『角度』で表現する『座標』もあるんです。
それが、『極座標(きょくざひょう)』。
一般の生活ではなかなか触れる機会がなかったのですが、
『プログラム』をやるにつれ必要になってきたので、
まるっとまとめてみることにしました。
極座標とは 直交座標系との違い
一般的な『座標』は、
『直交座標系(ちょっこうざひょうけい)』や『デカルト座標』とも呼ばれる『座標』になります。
- 横軸を $$ x $$
- 縦軸を $ y $
とすることが多いかなと思います。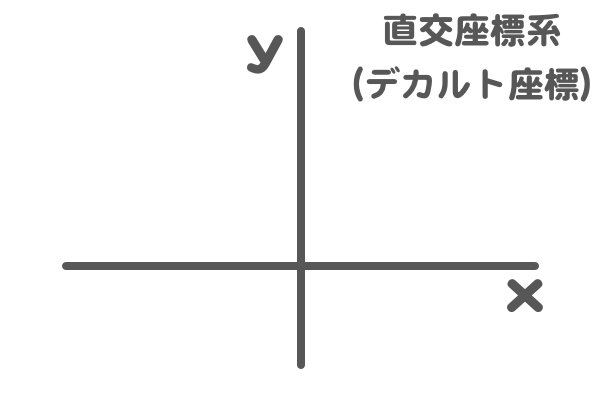
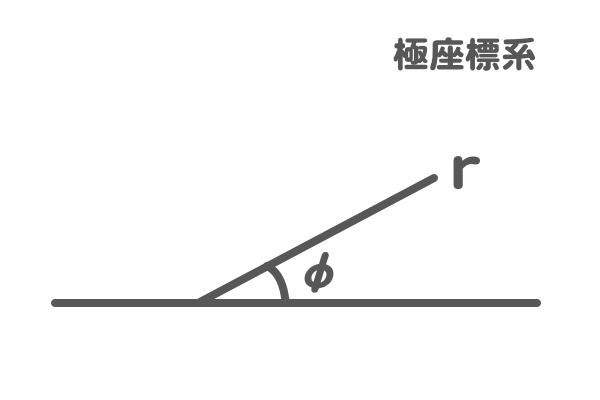
一方『極座標(きょくざひょう)』は、
『距離』と『角度』で物体の位置を表すことができる『座標』になります。
- 距離を$$ r $$ (アール)
- 角度を$$ \varphi $$(ファイ)
で書くことが多いようです。
と思ったりもするんですが、よくよく見てみると、
直線の周りをぐるっと一周しているようにみえなくもないかなぁと思いつつ、
大人の余裕でさらっと流すことにしておきます。
極座標のメリット らせんを書いたり 中心からの距離で表現したり
『極座標』を使ったグラフで面白い画像があったので紹介します。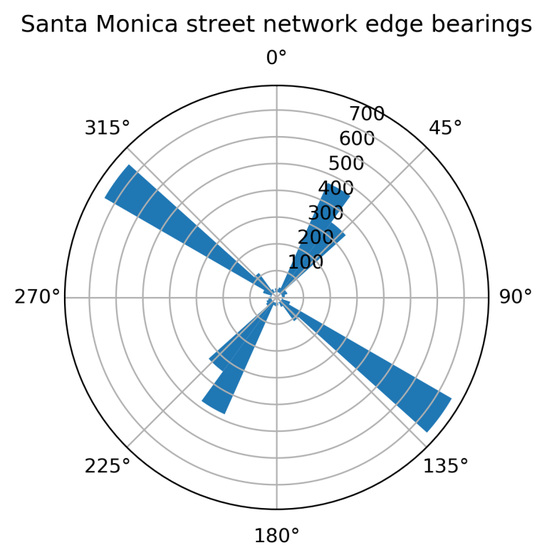
カリフォルニア州やボストンなどの都市部の高速道路が向いている方向を抽出し、
『極座標』で表現されています。
世界各都市の道路が向いている方角が可視化されたグラフを比べてみると何がわかるのか?
また、
色彩でおなじみの『HSL』も『極座標』で描かれています。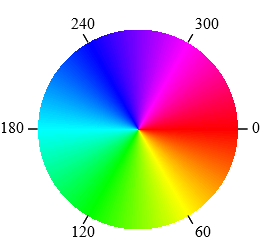
『HSL』の参考記事
音に関連する周波数を描いたグラフもありました。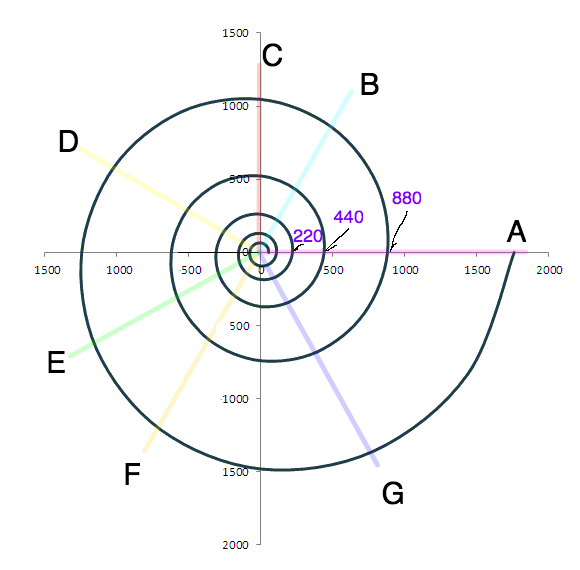
角度を変えながら描画するのは、縦横のグラフでは表現できない形かなと思います。
座標で知っておきたい『単位ベクトル』
『数学』でも『物理』でも、
『座標』で『ベクトル』を表現することがあります。
- ベクトル・・複数の値の組み合わせ。(xとyなど)
『ベクトル』の参考記事
『ベクトル』にはいくつか名称がありますが、
長さ1のベクトルを特に『単位ベクトル』と言います。
『X軸』の『単位ベクトル』を『$$e_x$$』として、
『Y軸』の『単位ベクトル』を『$$e_y$$』とすると、
$$ e_x = e_y = 1 $$
となります。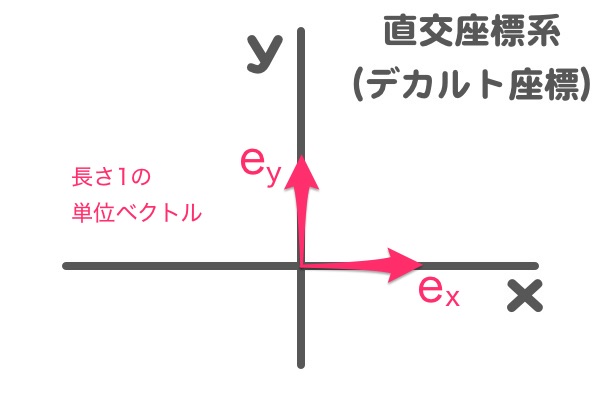
『極座標』にも『単位ベクトル』があって、
『r方向』の『単位ベクトル』を『$$e_r$$』として、
『φ(ファイ)』で動く方向の『単位ベクトル』を『$$e_\varphi$$』とすると、
$$ e_r = e_\varphi = 1 $$
になります。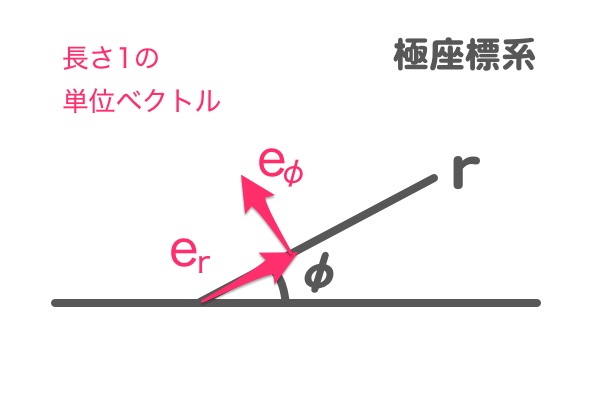
また、$$e_r$$ と $$ e_\varphi $$ は常に垂直の方向を向いているようです。
極座標から直交座標に変換してみる
『プログラム』の中には『極座標』で考えられているものがあって、
『極座標』から『直交座標系』に変換する作業が発生します。
変換する方法はというと、
まずは『極座標』と『直交座標系』を合わせます。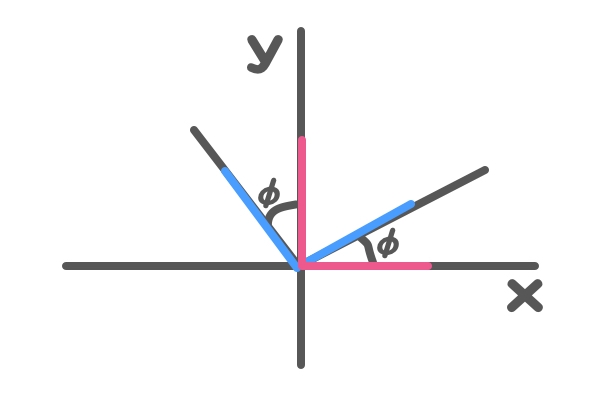
よくよく見れば、三角形が見えてくると思います。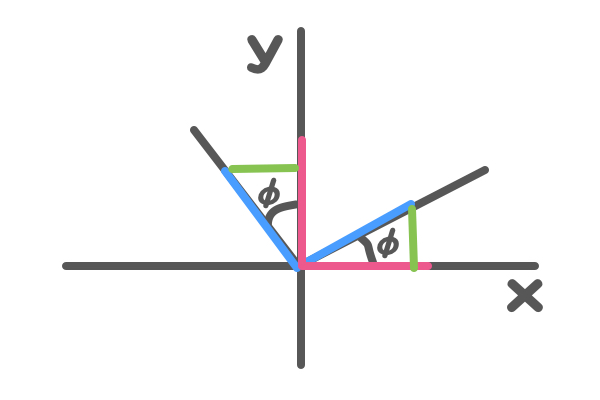
三角形といえば『三角関数』の出番ですね。
『三角関数』の関連記事
単位ベクトルで見ると、
$$ e_x = e_y = e_r = e_\varphi = 1 $$
になるので、半径1の円が描けるのもポイントかなと思います。

点$$e_r$$で考えると、
角度$$ \varphi $$と直角の三角形とみなせば、
横軸のピンクの線が$$\cos\varphi $$になって、
縦軸の緑の線が$$\sin\varphi $$になります。
点$$e_r = (\cos\varphi e_x, \sin\varphi e_y$$)
になります。
また、別の書き方として、
三角形の1辺を『$$r$$』とするとこう計算できるので、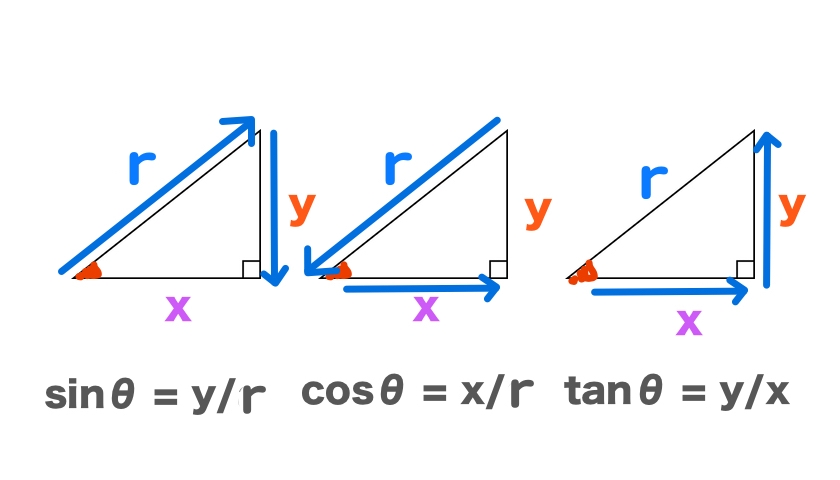
ちょっと形を変えると、
点$$e_r $$の $$x = r \times \cosθ$$
点$$e_r $$の $$y = r \times \sinθ$$
とも書けます。
これをプログラミングでも組み込めばOKということになります。
極座標を直交座標に変換するプログラム
せっかくなので簡単なプログラムを書いてみます。
遊ぶようにプログラムできる『P5.js(ProcessingのJavaScript版)』だとこんな感じになります。
See the Pen
p5.js sin-test-3d by aoki_monpro (@suica)
on CodePen.
コードはこんな感じ。
let r;
let theta;
function setup() {
createCanvas(200, 200);
r = 50;
theta = 0;
}
function draw() {
background(0);
//中心に移動
translate(width / 2, height / 2);
// ここで極座標->直交座標に変換
let x = r * cos(theta);
let y = r * sin(theta);
ellipseMode(CENTER);
noStroke();
fill(200);
ellipse(x, y, 20, 20);
theta += 0.1;
}
もちろんメインはこの部分。
// ここで極座標->直交座標に変換 let x = r * cos(theta); let y = r * sin(theta);
この形で計算できているのがわかるかと思います。
$$x = r \times \cosθ$$
$$y = r \times \sinθ$$
また、『極座標』→『直交座標系』に変換する前提で作られている
『バラ曲線』というものもあります。
『極座標』→『直交座標系』に変換する参考記事
極座標についてまとめてみて
XとYの軸ではなくて、
距離と角度で表現する『極座標』だからこそ表現しやすい事もあるようで、
調べつつ徐々に追加していきたいなと思います。
『数学・物理』関係ではこんな記事も読まれています。
1. 【P5.js】初心者向けの動画をリリースしました(プログラミング×数学物理)【Udemy】2. 【ベクトル】をわかりやすくするコツ〜『ベクトル』はただの数値の組み合わせです(4)【P5.js】
3. プログラムで数学も身につく 一石四鳥なクリエイティブコーディング
4. 【三角関数】の使い方〜わかりやすさ重視でまとめてみた【動画あり】
5. 【ラジアン】とは わかりやすくまとめてみた【初心者向け】
6. 【図解】波の用語や動きをプログラムも交えてまとめてみる【数学&物理】
7. 【微分】とは わかりやすくまとめてみた〜めっちゃすごいわり算【初心者向け】
8. 【シグマ(∑)】計算をわかりやすくまとめてみた【エクセルのsum】【初心者向け】
9. 【極座標 】とは【直交座標 】との違いや変換方法についてまとめてみた
10. 【虚数】【複素数】とは わかりやすくまとめてみた【初心者向け】
11. 【指数】とは わかりやすくまとめてみた【初心者向け】
12. 【対数】とは わかりやすくまとめてみた【初心者向け】
13. 順列・組み合わせ・階乗とは わかりやすくまとめてみた【数学】
14. 【確率(加法定理)】とは わかりやすくまとめてみた【初心者向け】
15. 【ベクトル場】と【速度ベクトル】とは わかりやすく【ドラクエのすべる床】
↓ ここから下は物理関連
1. プログラムで【加速度】をわかりやすくするために実際に動かしてみる(5)【P5.js】
2. 【流体力学】とは 圧力・密度・浮力をまとめてみた【初心者向け】
↓ ここから下はちょいムズカシイ
1. 【ネイピア数】とは わかりやすくまとめてみた【自然対数の底(e)】
2. 【ベクトル解析 勾配(grad)】わかりやすくまとめてみた
3. 【ベクトル解析 発散(div)】わかりやすくまとめてみた
4. 【テイラー展開】をわかりやすくまとめてみた【おすすめ動画あり】
アオキのツイッターアカウント。




















この記事へのコメントはありません。