学校の勉強で、

『なんのために勉強するのかわからないランキングTOP3』

に堂々入ってきそうな授業といえば。

そう。

『微分(びぶん)』と『積分(せきぶん)』。

実際、社会人になって十数年 生活する中で、

まったくもって使う機会はなかったけれど、

子どもが産まれて、最近の『STEAM教育』を調べるうちに、

どうやらめちゃくちゃ使うらしいという事に今更ながら知る事になりました。

• AI・機械学習
• 統計学
• 経済学
• 3Dプログラミング(ゲーム、シミュレータ、VR/AR/MR)
• 物理学
• 機械工学

などの分野では『微分』『積分』は必須だそうで。

他にも、

• プロ野球でホームラン打った時の到達距離予測
• 台風の進路予測
• 株価の動き予測
• 大砲うったときの到達場所予測

などなど。

現に、『3Dプログラミング』でかっこいい映像をつくろうと調べ出したら、

どこもかしこも『微分』『三角関数』『ベクトル』のオンパレードで。

ということで、『微分』のさわりだけ、まとめてみることにしました。

わかりやすさ重視で書いていますので、ぜひ寛大な心でお読みください。

微分をわかりやすく〜そもそも『微分』ってなんなのさ

そもそも『微分(びぶん)』ってなんなのさってことで調べてみると、

『微(び)』という漢字は、『とっても小さい』という意味があります。

• 微生物(びせいぶつ)
• 微妙(びみょう)
• 微力(びりょく)
• 微熱(びねつ)
• 微量(びりょう)
• 微調整(びちょうせい)
• 微笑(びしょう)
• 顕微鏡(けんびきょう)
• 微増(びぞう)

などなど。

『微分(びぶん)』の『分(ぶん)』はそのまま『分ける』という意味なので、

『微分』 = めっちゃ小さく分ける

という理解でいいのかなと。

どれくらい小さいかというと、例えば、

長さ20センチメートルのロールケーキがあったとして、

3等分とか、6等分とかのレベルじゃなくて、

300等分とか1000等分とかに分けるような感じでしょうか。

って思っちゃうんですが、

とにかくひたすら小さく分けて、どれくらい変化したのかを考えようというのが『微分(びぶん)』になります。

ちなみに、

『微分』の反対が『積分(せきぶん)』で、
めっちゃ小ちゃいものをくっつけるのが『積分(せきぶん)』になります。

• 『微分(びぶん)』・・めっちゃすごい割り算
• 『積分(せきぶん)』・・めっちゃすごいかけ算

みたいな関係になります。

微分をわかりやすく〜ほとんどゼロやん・・極限

例えば20センチのロールケーキを3等分にするなら、

20 ÷ 3 = 6.666 (約6センチずつ) になります。

例えば5等分にするなら、

20 ÷ 5 = 4センチずつ になります。

もし300等分ができるとしたら、

20 ÷ 300 = 0.066 (0.66ミリ) ずつに分ければ、

300等分できることになります。

もし1000等分なら、

20 ÷ 1000 = 0.02 (0.2ミリ)

になります。

目ではほとんど見えないけれど、

顕微鏡で見たらかすかに見えるみたいな状態を、

『極限(きょくげん)』と呼ぶそうで、英語で『Limit(リミット)』と呼びます。

微分をわかりやすく 割り算と微分の違い

ロールケーキの例で、300等分や1000等分してみましたが、
ロールケーキを分けるだけなら、割り算で計算することができます。

• 割り算・・一定の値で割る (2で割ったり5で割ったり)
• 微分・・ほとんどゼロに近い 2点の差(変化量)を割る

という違いになります。

自動車で例えると、

もし自動車が、ずーーーっと同じスピードで走っていたら、割り算で距離や時間を出せますが、

実際にはアクセルを踏んだりブレーキをふんだりするので、スピードが変わったりしますよね。

その時々のスピードを知りたいとしたら、一瞬一瞬の変化を見る必要がでてきます。

一瞬一瞬の変化を見るには、2つ地点の差を見ればわかる、ということになります。

例えば、

2秒と2.001秒の差は、2.001 – 2 = 0.001 になります。

この間の速度を0.001で割れば、2秒と2.001秒の間の速度がわかることになります。

式にするとこんな感じです。

一瞬の変化 $ \displaystyle = \frac{2.001秒時の速度 – 2秒時の速度}{0.001秒} $

微分をわかりやすく グラフにしてみる

自動車がアクセルを踏んだりブレーキを踏んだりした様子をグラフにしてみました。

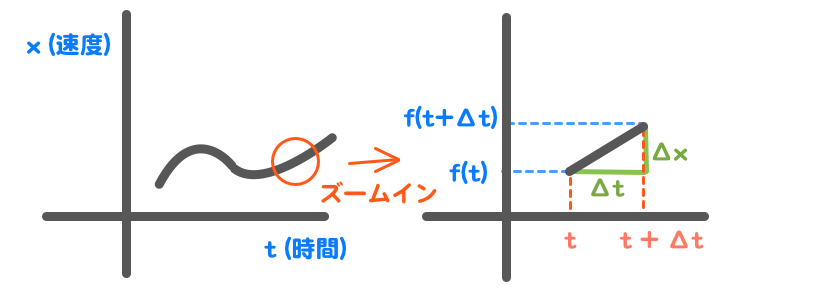
横軸が時間で、縦軸が速度になります。

ある瞬間(t)の速度と、
ちょっとだけ進んだ時 (t + Δt)(ティープラスデルタティー) の速度の2点を、
ギリギリまで近づけて、式を出しています。

• t・・Timeの頭文字。 例えば2秒とか
• t+Δt・・tにほんのちょっとだけ加えた数値。例えば 2.0001秒とか。

瞬間の速度 $ \displaystyle = \lim_{\Delta t\rightarrow 0}\frac{\Delta x}{\Delta t}
$

limはリミットで極限。
limの下は、Δt (デルタティー) を ギリギリまで0に近づけるという意味になります。

(xは速度、tは時間、Δ(デルタ)はほんのちょっとだけというような意味です。)

また、ギリギリまで近づけたという意味も込めて、
リミットの式はこんな風に書き換えることができます。

瞬間の速度 $ \displaystyle = \frac{dx}{dt} $

dは英語で『difference( ディファレンス)』の略で、差分や変化という意味になり、

極限まで小さくした変化という意味になります。

$ \displaystyle \frac{dx}{dt} $の式を

『xをtで微分する』と呼ぶそうです。

※ dx や dt が一つの記号なので、 dとxを切り離すということはできないです。

微分をわかりやすく 微分の解き方(短めと長め)

『微分』の解き方を短めと長めで書いてみます。

まずは短め。

『指数(2の2乗など)』があったら『指数』を前に降ろしつつ、『指数』を1減らせばOKになります。

仮に $ x=\displaystyle t^2 $ という式があって、『tで微分』すると、

$ t^2 $ の2が降りてきて、$ t^2 $の2乗が1減るので、

$ \displaystyle \frac{dx}{dt} = 2t $ になります。

続いて長め。

2点間(tとt+Δt)の差を表すとこう書けます。
$ \displaystyle \frac{dx}{dt} = \lim_{\Delta t\rightarrow 0}\frac{f(t+\Delta t) – f(t)}{\Delta t} $

$ x = t^2 $ ということは、式にすると $ f(x) = t^2 $ と書けるので、

$x $があたる箇所に$ t^2 $ を代入します。

$ \displaystyle \frac{dx}{dt} = \lim_{\Delta t\rightarrow 0}\frac{(t+\Delta t)^2 – t^2}{\Delta t} $

2乗を展開します。

$ \displaystyle \frac{dx}{dt} = \lim_{\Delta t\rightarrow 0}\frac{t^2+2t\Delta t + (\Delta t)^2 – t^2}{\Delta t} $

分子に $ t^2 $ が2つあり、引き算になるので消します。

$ \displaystyle \frac{dx}{dt} = \lim_{\Delta t\rightarrow 0}\frac{2t\Delta t + (\Delta t)^2 }{\Delta t} $

分母にある $ \displaystyle \Delta t $をそれぞれ割ります。

$ \displaystyle \frac{dx}{dt} = \lim_{\Delta t\rightarrow 0}(2t + \Delta t ) $

$ \displaystyle \Delta t $を限りなく0に近づけます。(0なのでなくなります。)

$ \displaystyle \frac{dx}{dt} = 2t $

なので、 $ x=\displaystyle t^2 $ を『tで微分』すると、 $ x=\displaystyle 2t $
になります。

微分をわかりやすく 面積と円周、距離と速度

実は『円』の面積を半径で『微分』すると、『円周の長さ』になります。

円の面積 $y = \pi r^2 $

円周の長さ $ y’ = 2 \pi r $

『球』の体積も、『微分』すると『球の表面積』になります。

球の体積 $ y = \frac{4\pi r^3}{3} $

球の表面積 $ y’ = 4 \pi r^2 $

実は、距離を『微分』すると速度になって、速度を『微分』すると加速度になります。

距離 $ y = x^2 $

速度 $ y’ = 2x $

加速度 $ y” = 2 $

※微分した印として『'(プライム)』をつけています。2回微分なら『”(ダブルプライム)』です。

微分をわかりやすく 補足としてのハイクオリティ動画のご紹介

文章だけだとどうしてもわかりづらいと思うので、

とにかくおすすめの動画があるのでご紹介します。

教育系ユーチューバー『ヨビノリたくみ』さんの『微分積分』の動画です。

講義としては約1時間ちょい、質疑応答入れて1時間40分くらいの動画なのですが、

『微分』のビの字も知らない方達に向けてわかりやすい講義をしています。

41分くらいから微分の話になっています。

動画の内容が本にもなっています。

微分をわかりやすく 偏微分(一つずつ微分します)

『微分』の仲間的な存在に、『偏微分(へんびぶん)』というものがあります。

『偏微分』は日本語だとわかりづらいんですが、

英語にすると『partial(パーシャル・一部分)』という意味を表していて、

• まずXだけを微分して、(Yは0として扱う)
• 次にYだけを微分して、(Xは0として扱う)

といったように、いっぺんに微分するのではなく一つ一つ『微分する』手法になります。

『偏微分』を表す記号は『$ \partial $(ラウンド)』。

• ラウンド、ディー、パーシャルなどいくつかの呼び名があります。

こちらもヨビノリたくみさんのわかりやすい動画があるのでぜひ。

『偏微分』を使う関連記事

微分をわかりやすく プログラミングの活用事例

『微分』の『プログラミング』での活用事例としては、

『機械学習』でしょっちゅう使われますが、『3Dプログラミング』でもよく使われています。

例えば、

球体に光をあてて、どれくらい反射しているかというのを計算する際に、

『微分』の考え方を使っています。

関連記事

微分をわかりやすく まとめ

学校で勉強していた頃は、

という疑問がずっとでていて、実際に使う機会もそうそうなかったのですが、

しっかりと現実世界を見て、
そこで使われている技術を知っていくうちに、

という事に気づいたりします。

そのためにはもっと、現実世界と学校の勉強を連動させる必要があると思うので、

これからもこのブログなり、
子供向けプログラミング道場『CoderDojo熊本』を通じて、
現実世界との連動をメインテーマに活動していきたいなと思います。

PS. マンガでわかる微分積分もわかりやすいのでオススメ本です。

『数学・物理』関係ではこんな記事も読まれています。

1. 【P5.js】初心者向けの動画をリリースしました(プログラミング×数学物理)【Udemy】

2. 【ベクトル】をわかりやすくするコツ〜『ベクトル』はただの数値の組み合わせです(4)【P5.js】

3. プログラムで数学も身につく 一石四鳥なクリエイティブコーディング

4. 【三角関数】の使い方〜わかりやすさ重視でまとめてみた【動画あり】

5. 【ラジアン】とは わかりやすくまとめてみた【初心者向け】

6. 【図解】波の用語や動きをプログラムも交えてまとめてみる【数学&物理】

7. 【微分】とは わかりやすくまとめてみた〜めっちゃすごいわり算【初心者向け】

8. 【シグマ(∑)】計算をわかりやすくまとめてみた【エクセルのsum】【初心者向け】

9. 【極座標 】とは【直交座標 】との違いや変換方法についてまとめてみた

10. 【虚数】【複素数】とは わかりやすくまとめてみた【初心者向け】

11. 【指数】とは わかりやすくまとめてみた【初心者向け】

12. 【対数】とは わかりやすくまとめてみた【初心者向け】

13. 順列・組み合わせ・階乗とは わかりやすくまとめてみた【数学】

14. 【確率(加法定理)】とは わかりやすくまとめてみた【初心者向け】

15. 【ベクトル場】と【速度ベクトル】とは わかりやすく【ドラクエのすべる床】

↓ ここから下は物理関連

1. プログラムで【加速度】をわかりやすくするために実際に動かしてみる(5)【P5.js】

2. 【流体力学】とは 圧力・密度・浮力をまとめてみた【初心者向け】

↓ ここから下はちょいムズカシイ

1. 【ネイピア数】とは わかりやすくまとめてみた【自然対数の底(e)】

2. 【ベクトル解析 勾配(grad)】わかりやすくまとめてみた

3. 【ベクトル解析 発散(div)】わかりやすくまとめてみた

4. 【テイラー展開】をわかりやすくまとめてみた【おすすめ動画あり】

アオキのツイッターアカウント。