『プログラム』でかっこいい映像をつくろうと『シェーダー』をやってみたり、
『機械学習』や『統計学』を調べると必ずと言っていいほど目にするキーワードがあります。
それは『ネイピア数』。
英語で『Napier’s constant』。
別名『自然対数の底』(Natural logarithm)。
記号『e』で表すと。
ということで今回は、
『ネイピア数』についてまとめてみることにしました。
ネイピア数をわかりやすく 由来
『ネイピア数』の由来について色々ググってみると、
- 1618年に『ジョン・ネイピア』が発表した研究の付録に記録されていて、
- 『ヤコブ・ベルヌーイ』が複利の計算で見出して、
- 『ゴットフリート・ライブニッツ』が定数の記号(当時はb)をつけて
- 1727年から『レオンハルト・オイラー』が記号eを使い始めた
そうです。
記号『e』の由来は諸説あるようですが、
『指数(exponential)』の頭文字をとったというのが有力のようです。
ネイピア数をわかりやすく 複利の計算で生まれた
『ヤコブ・ベルヌーイ』が発見した『複利の計算』を実際にやってみます。
1年で100%の金利をつけてくれる銀行があったとします。
1年で100%増えるので、1年後には合計2万円になると。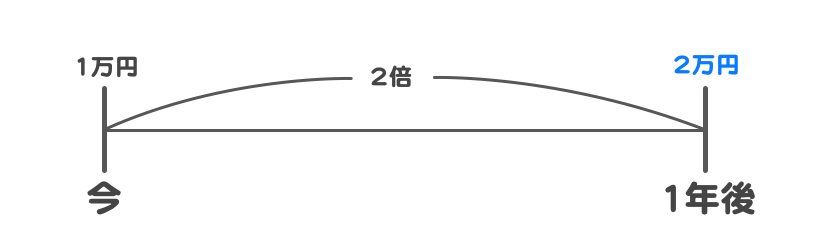
では例えば、半年で50%、もう半年で50%増えるとすると・・
こうなります。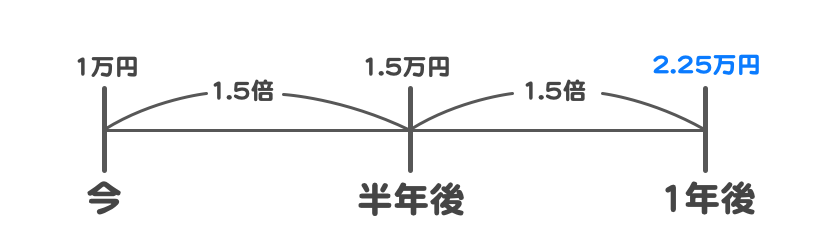
例えば3ヶ月おき(4分の1おき)にしたら・・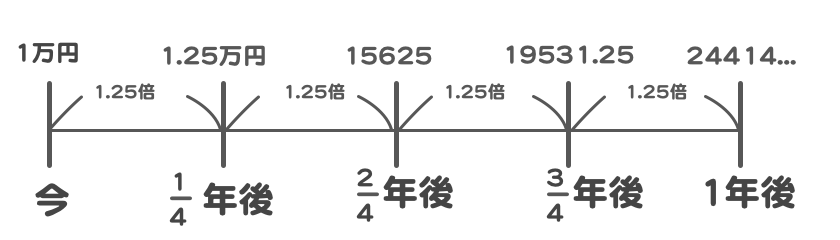
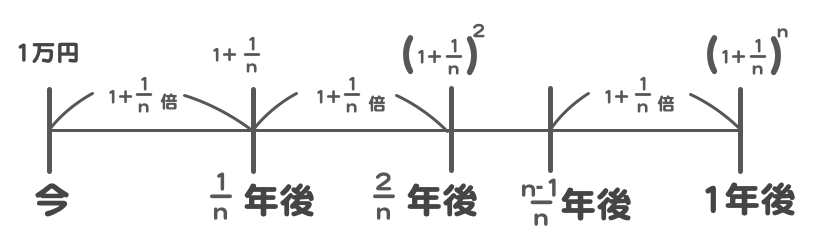
計算を繰り返すうちに、
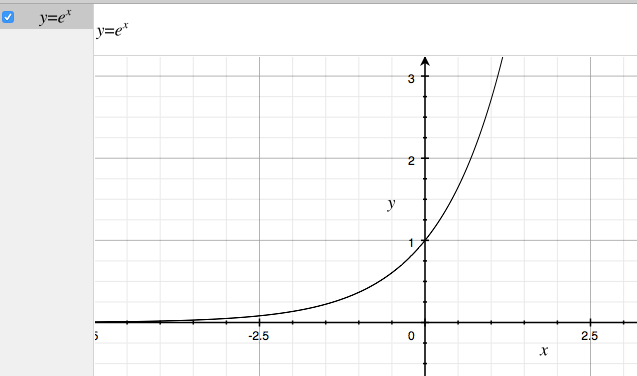
- 『e』・・2.71828・・・(延々続く無理数)
ということがわかったそうです。
※当時は『e』ではなく、極限で表記していたようです。『e』とつけたのは『レオンハルト・オイラー』。
$$\displaystyle \lim_{n \rightarrow \infty}(1 + \frac{1}{n})^n $$
- 極限・・ギリギリまで矢印の方向(この場合は∞)に近づける
『極限』に関する参考記事
グラフにするとこうなります。
ネイピア数は微分してもネイピア数だって!?
『ネイピア数』には不思議な性質があって、
なんと、『微分』しても『ネイピア数』のまま(!)になります。
$$ (e^x)′=e^x $$
色々ググって計算方法を見つけてきました。
微分の定義にあてはめて色々計算していくと、
結局もとの値と同じという結果になるようです。
1.『微分の定義』にあてはめる。
$$ (e^x)’ = \displaystyle\lim_{h \rightarrow 0}\frac{e^{x+h} – e^x}{h} $$
2.『指数の法則』で$$e^{x+h}$$を変形。
$$ (e^x)’ = \displaystyle\lim_{h \rightarrow 0}\frac{e^xe^h – e^x}{h} $$
3.分子を$$e^x$$でくくる。
$$ (e^x)’ = \displaystyle\lim_{h \rightarrow 0}\frac{e^x(e^h – 1)}{h} $$
4.$$e^x$$を前にだす。
$$ (e^x)’ = \displaystyle e^x\lim_{h \rightarrow 0}\frac{e^h – 1}{h} $$
5.limより右はネイピア数eの定義の式と同じ。(limの後ろは1)
$$ \displaystyle \lim_{h \rightarrow 0}\frac{e^h – 1}{h} = 1 $$
という訳で、この式がなりたつようです。
$$ (e^x)′=e^x $$
参考記事
ネイピア数の意味
『微分』の参考記事
ネイピア数をわかりやすく 用途 具体例
『ネイピア数』は別名『自然対数の底』とも言われています。
『対数』の参考記事
と思いググってみると、いろんな活用事例が見つかりました。
- 1/nの確率で当たるくじ
- 2つのトランプのカードが一致する確率
- 秘書問題(応募者が採用できる確率)
- 正規分布やポアソン分布
- 放射性物質の半減期
- 化学反応における物質濃度の半減期
- お湯の冷却温度の変化
- マルサスモデル(生物の個体数などの増加や減少)
- 対数螺旋(カタツムリ、牛のツノ、台風など)
参考記事
ネイピア数は身近な数学的な問題の中でどのように現われてくるのか
実際の社会における自然現象等の表現において、どのように現れてくるのか
統計、確率、化学、物理などなど、幅広く使われているようです。
ネイピア数をわかりやすくまとめてみて
学生時代にはなんのこっちゃだった『ネイピア数』ですが、
- 統計学
- メディアアート
などの分野で使われていることを知り、深掘りしていると、
文字通りいろんな業界で使われているということに改めて気づかされました。
手計算だとややこしやですが、
幸い『パソコン』でちゃちゃっとやるとざざっと計算してくれるので、
少しずつ使ってみながらその性質をちょっとずつでも覚えていきたいもんです。
『数学・物理』関係ではこんな記事も読まれています。
1. 【P5.js】初心者向けの動画をリリースしました(プログラミング×数学物理)【Udemy】2. 【ベクトル】をわかりやすくするコツ〜『ベクトル』はただの数値の組み合わせです(4)【P5.js】
3. プログラムで数学も身につく 一石四鳥なクリエイティブコーディング
4. 【三角関数】の使い方〜わかりやすさ重視でまとめてみた【動画あり】
5. 【ラジアン】とは わかりやすくまとめてみた【初心者向け】
6. 【図解】波の用語や動きをプログラムも交えてまとめてみる【数学&物理】
7. 【微分】とは わかりやすくまとめてみた〜めっちゃすごいわり算【初心者向け】
8. 【シグマ(∑)】計算をわかりやすくまとめてみた【エクセルのsum】【初心者向け】
9. 【極座標 】とは【直交座標 】との違いや変換方法についてまとめてみた
10. 【虚数】【複素数】とは わかりやすくまとめてみた【初心者向け】
11. 【指数】とは わかりやすくまとめてみた【初心者向け】
12. 【対数】とは わかりやすくまとめてみた【初心者向け】
13. 順列・組み合わせ・階乗とは わかりやすくまとめてみた【数学】
14. 【確率(加法定理)】とは わかりやすくまとめてみた【初心者向け】
15. 【ベクトル場】と【速度ベクトル】とは わかりやすく【ドラクエのすべる床】
↓ ここから下は物理関連
1. プログラムで【加速度】をわかりやすくするために実際に動かしてみる(5)【P5.js】
2. 【流体力学】とは 圧力・密度・浮力をまとめてみた【初心者向け】
↓ ここから下はちょいムズカシイ
1. 【ネイピア数】とは わかりやすくまとめてみた【自然対数の底(e)】
2. 【ベクトル解析 勾配(grad)】わかりやすくまとめてみた
3. 【ベクトル解析 発散(div)】わかりやすくまとめてみた
4. 【テイラー展開】をわかりやすくまとめてみた【おすすめ動画あり】
アオキのツイッターアカウント。


















とてもわかりやすかったです!すこしだけ数学が好きになれました
ありがとうございます!