『なんのために勉強しているかわからないランキング』
があったら堂々トップ3には入ってきそうな『三角関数』。
高校生の頃は文字通り、なんのためにやっているかまるでわかっていなかったんですが、
子ども向け無料プログラミング道場『CoderDojo熊本』向けに、
スクラッチのその先へ
というお題で数学や物理を改めて学習しているうちに、
ということに今更ながら気づかされて。
という気持ちで、
難解と思われる『三角関数』を、できるだけ紐解いて書いていこうと思います。
関連記事:『スクラッチ』で『三角関数』の使い方
三角関数とは わかりやすく〜そもそもXとYってなんなのさ
中学数学あたりからでてくるXとY。
数学では一般的に、
- X軸は横
- Y軸は縦
とで表すようになっています。
教科書の中でしか出番がないかと思いきや、実は現実社会でこれでもかと使われています。
身近なところでいうと、『グーグルマップ』。
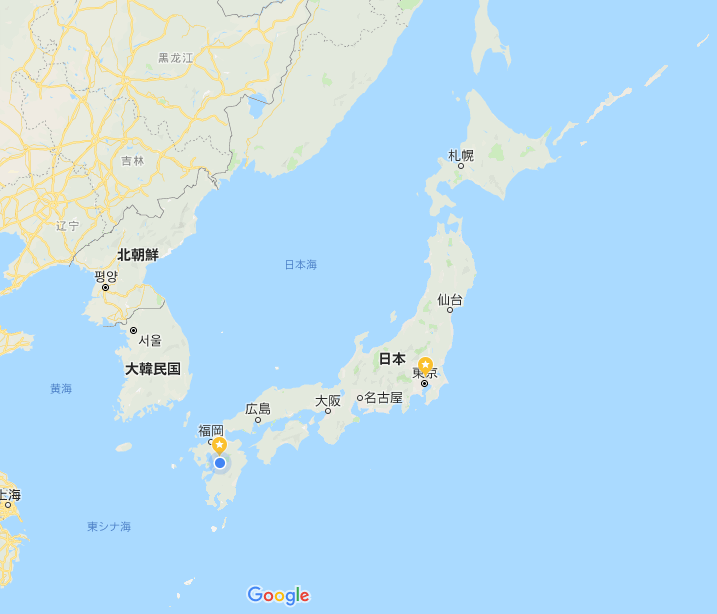
いわゆる地図ですが、
地図は平面で書かれているので、
世界中どんな場所でもXとYで位置を特定できるということになります。
ググってみたらこんなサイトがありました。
試しに『熊本城』で検索してみると、
- 経度・・130.705833
- 緯度・・32.806185
と表示されました。
『松本城』だと、
- 経度・・137.968955
- 緯度・・36.238652
と表示されました。
細かい数字はおいておいておきますが、ようは、
縦と横の数字を使うことで、『熊本城』でも『松本城』でも場所を特定できるということですね。
カーナビでおなじみの『GPS』も同じような仕組みで、
教科書の中だけしか活躍の場がないと思っていたXとYですが、
実は地球規模の位置特定システムなんかにも使われているすごい仕組みなんです。
三角関数とは わかりやすい由来〜現実世界の測量をするために誕生
サインコサインタンジェントという魔法のような名前だけは覚えている『三角関数』。
これまた学校の教科書の中だけで使われているかと思いきや、
現実世界でこれでもかといわんばかりに活用されています。
- 測量・・GPS、地図、土木工学、精密機械工学、ケーキカット
- 回転・・ゲームプログラミング、CG、航法、機械工学、宇宙機や航空機の姿勢制御
- 波・・ 音声処理、画像処理、ノイズフィルター、振動工学、量子力学などさまざまな物理学分野
- その他・・内積、コサイン類似度、ボックス=ミュラー法(正規乱数の生成)、カーネル法における非線形関数としてなど
参考
三角関数は何に使えるのか 〜 サイン・コサイン・タンジェントの活躍 〜
とはいえいきなりサインコサインタンジェントの公式を丸暗記してもナンジャラホイとなってしまうので、
そもそもなぜに三角関数は生まれたのか、っというところから調べてみると、よさげな記事がありました。
ようは、2000年以上前に、現実世界の測量のために生まれたようです。
いやーすごい。
これ考えたヒッパルコスさんハンパない。
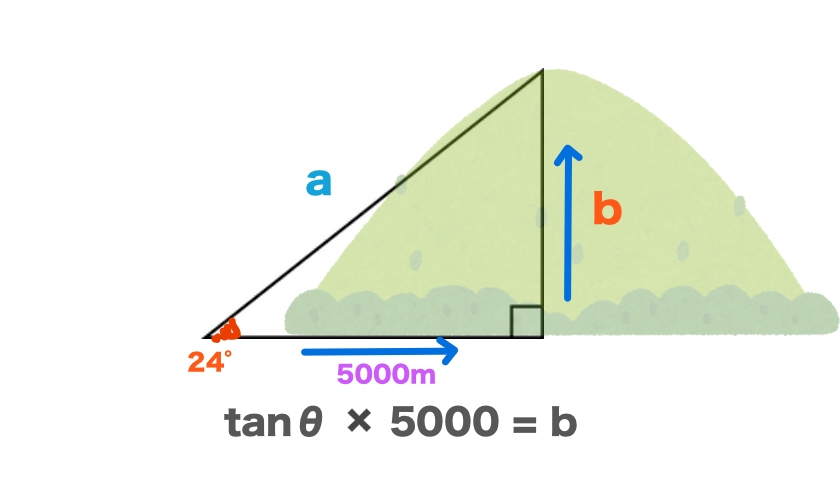
2つの角度が同じなら、大きさは違っても形はかわらないという三角形の法則と、
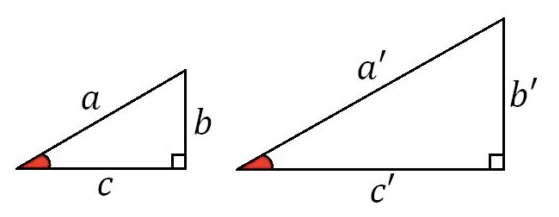
2つの角度(直角90度ともう一つの角度)と1つの長さがわかれば、
もう一方の長さも計算できちゃうという『三角関数』を使いこなして、
- 遠くの山の高さを測ったり、
- 地球の半径を測ったり、
- 月までの距離を測ったり、
ということもできるようになったと。
三角関数とは わかりやすい使い方〜XとYに置き換えてみる
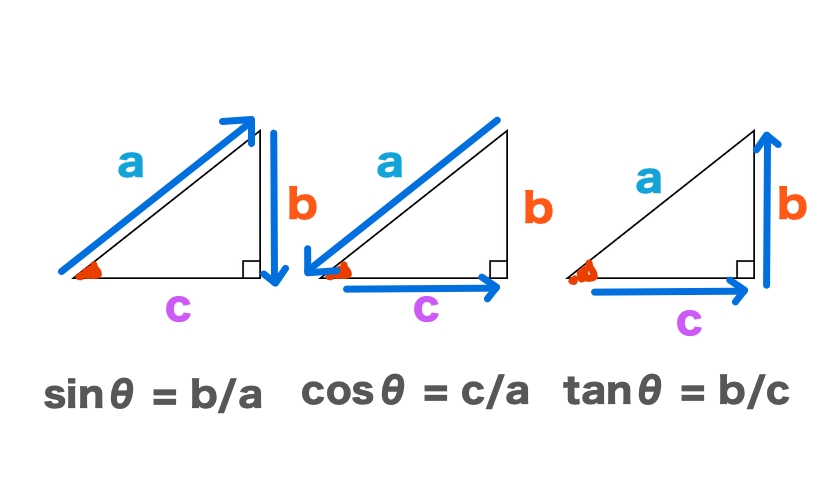
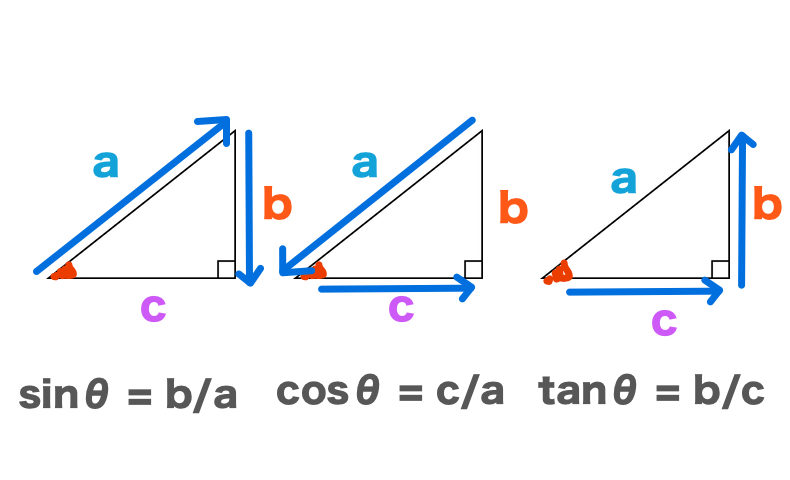
ここで改めて、数学の教科書でもおなじみのサインコサインタンジェントの式をば。

教科書でおなじみの書き方だと、a,b,c とついちゃってるのが多いのですが、
プログラミングでも使いやすいように、
横軸はx、縦軸はy
としつつ、
あとで説明しますが、aはrと書き換えておきます。
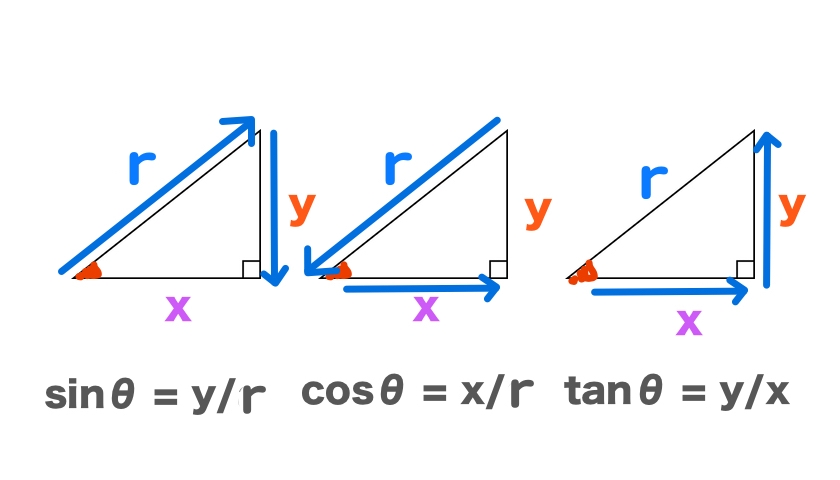
- 横が x
- 縦が y
- ななめが r (rはradius(ラディウス)の略、日本語で半径という意味)
ですね。
- サイン・・rの長さと角度がわかれば、yの長さ(縦軸の長さ)がわかる
- コサイン・・rの長さと角度がわかれば、xの長さ(横軸の長さ)がわかる
- タンジェント・・xの長さ(横軸の長さ)と角度がわかれば、yの長さ(縦軸の長さ)がわかる
という意味になります。
計算の方法は、
分数の計算の仕方は小学校で習ったかどうか・・?、なのですが、
イコールの左側(左辺)と、イコールの右側(右辺)両方に、分母の数をかけ算するとOKです。
例えばサインならこんな流れ。
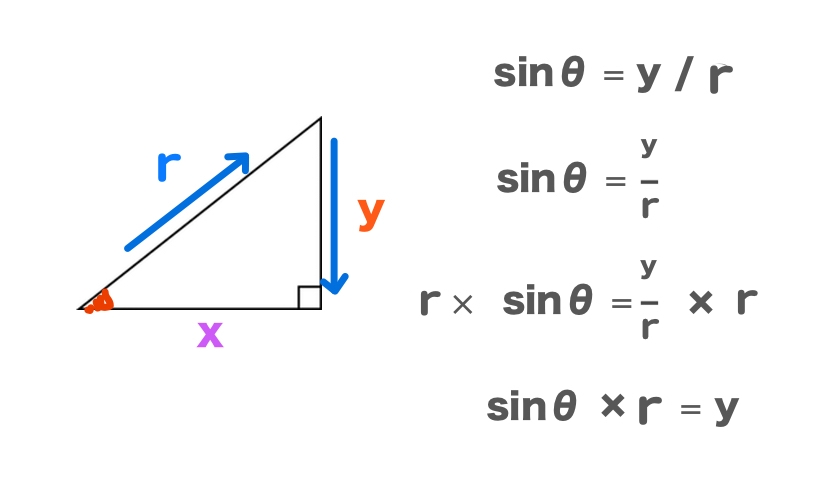
イコールの左側(左辺)と、イコールの右側(右辺)両方に r をかけて、分母がなくなると(正確には1なのですが気にしない)。
で、
- 角度が30度ならサイン(sinθ)は 0.5
- 角度が60度ならサイン(sinθ)は 0.866
- 角度が90度ならサイン(sinθ)は 1
と、角度に合わせて対応する数字が決まっているのですが、
これは2000年前にヒッパルコスさんが法則を見つけていたそうで、『三角比の表』というものがあります。
と思っていろいろ調べてみたところ、
どうやら『円』と組み合わせてみるとわかりやすいようです。
三角関数のわかりやすい使い方〜三角だけど円で見るとわかりやすい
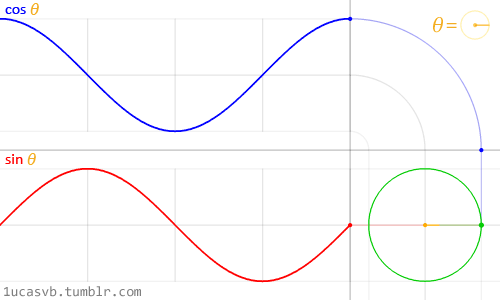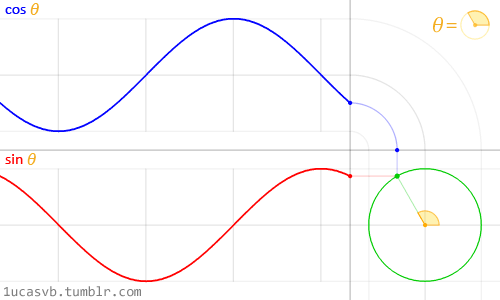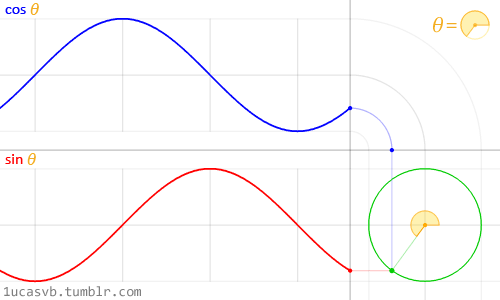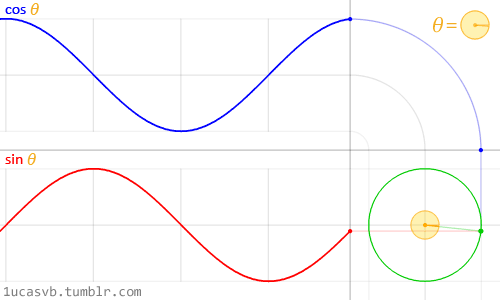
三角形と『円』を組み合わせた図がこちら。
まずは『サイン(sinθ)』。
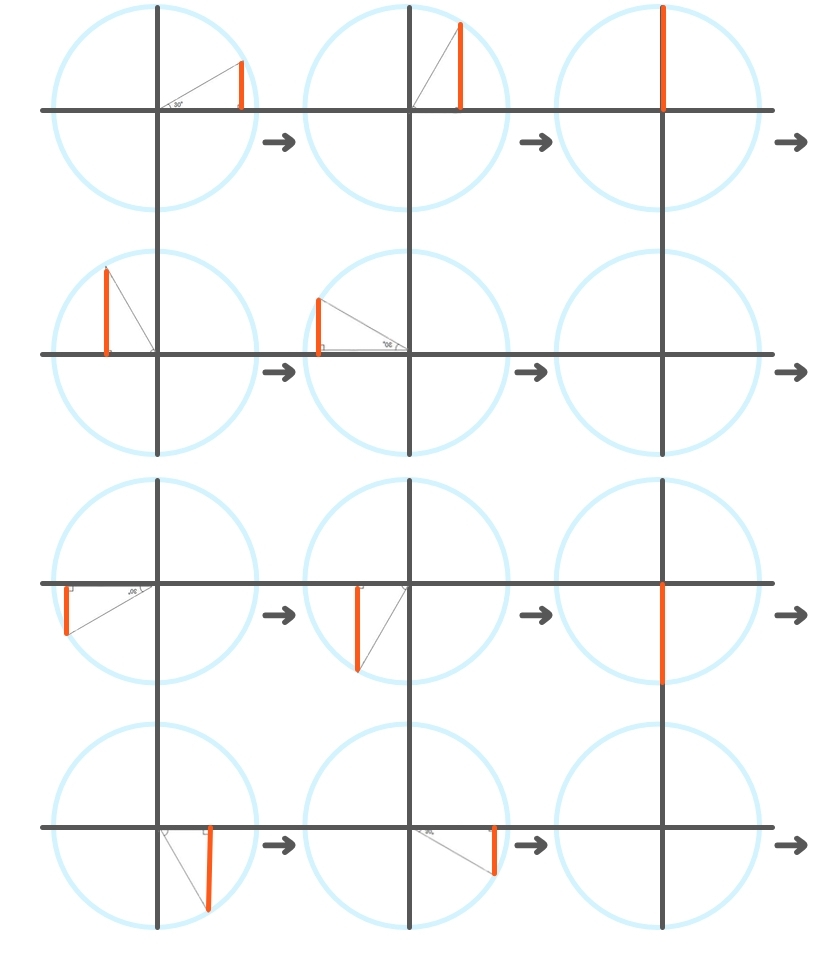
左上から右に向かって見ていきます。
1段目:三角形の角度が、30度→60度→90度 と変わると、オレンジの線の長さが伸びていきます。
ちょうど90度で、半径とぴったりになります。
2段目:120度→150度→180度で、オレンジの線が短くなり、180度で0になります。
同じように、
3段目は270度でオレンジの線が半径とぴったりになり、
4段目、360度(0度)でオレンジの線が0になります。
仮にこの円の半径を『1』とすると、
- 0度・・・0
- 90度・・・1
- 180度・・・0
- 270度・・・-1
- 360度(0度)・・0
という風に変わっていきます。
これがサイン(sinθ)の値になります。
次に『コサイン(cosθ)』。
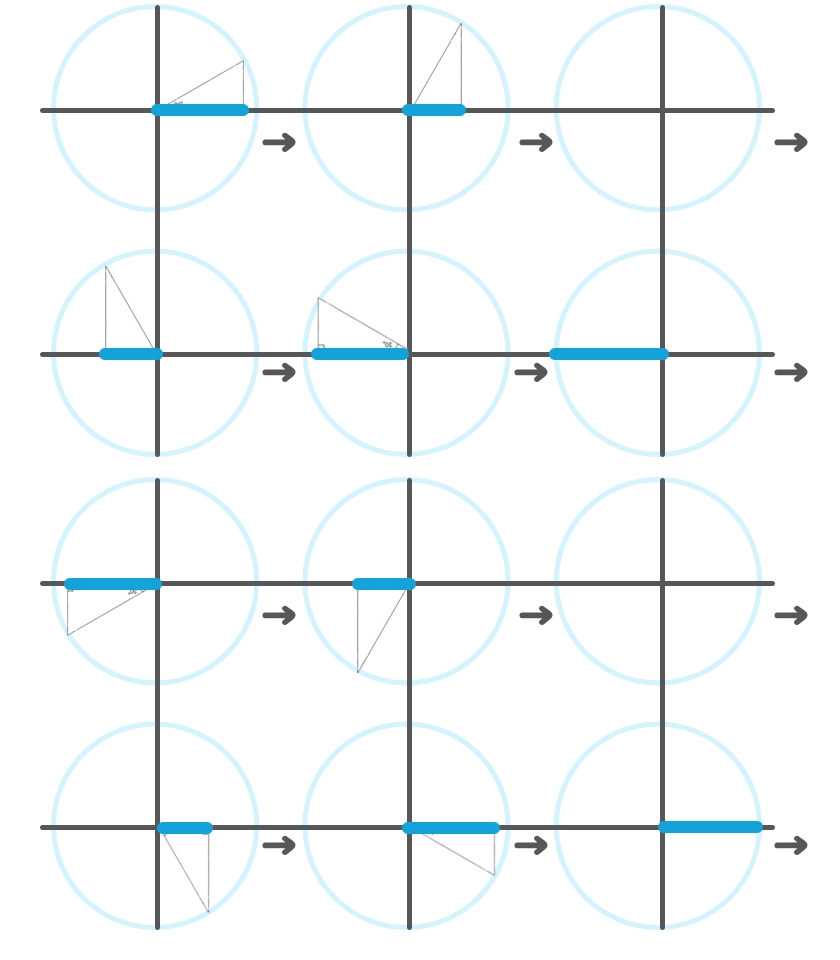
こちらも左上から右に流れていきます。
0度の時が青い線が一番長くて、
30度→60度と変わるうちにだんだん短くなって、
90度で青い線が0になります。
2段目:ちょっとずつ青い線が伸びていって、180度で一番長くなります。
仮にこの円の半径を『1』とすると、
- 0度・・・1
- 90度・・・0
- 180度・・・-1
- 270度・・・0
- 360度(0度)・・1
という風に変わっていきます。
これがコサイン(cosθ)の値になります。
なめらかに動かすとこんな感じになります。
ちなみに・・『タンジェント(tanθ)』はちょっと特殊な動きをするので今回は省きます。
これらの計算を手でやるとなかなか大変なんですが、
プログラミングを使うと『三角比の表』が手元になくても簡単に計算できて、なんなら動かすこともできるようになります。
三角関数をスクラッチで~サインコサインを使ってみる
せっかくなので、試しに『スクラッチ』でやってみました。
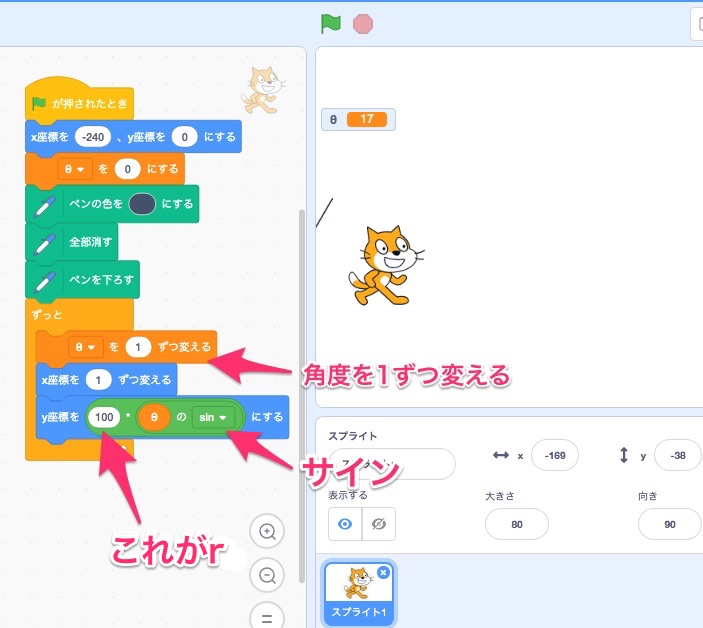
サインの場合、
- サイン・・r(半径)の長さと角度(θ)がわかれば、yの長さ(縦軸の長さ)がわかる
rというのは、『円』で考えれば半径の長さになります。
という事で、r(半径)の値を適当に100として動かして、角度(θ)を1ずつ増やしています。
わかりやすいように横軸(X)も1ずつ増やしてみます。
動画だとこんな感じになります。
角度が増えるほど、高さ(Y軸)が100に近づいていって、
- 90度の時に高さ(Y軸)が100になって、
- 180度の時に高さが0になって、
というような動きをしています。
また、サインとコサインを組み合わせると、
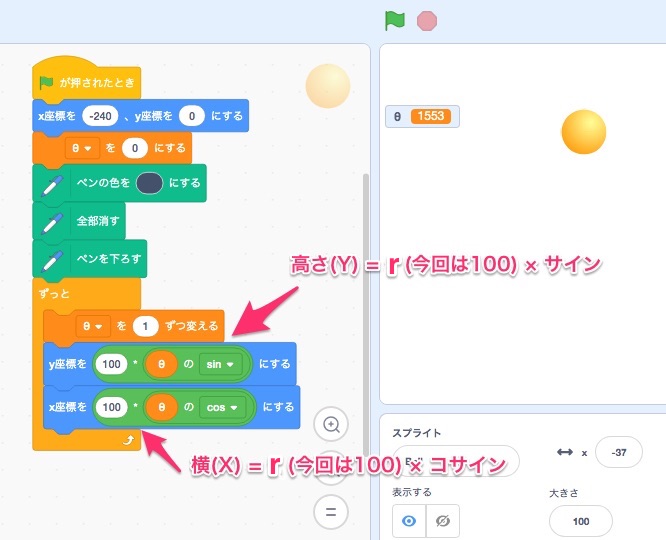
- サイン・・r(円の半径)の長さと角度がわかれば、yの長さ(縦軸の長さ)がわかる
- コサイン・・r(円の半径)の長さと角度がわかれば、xの長さ(横軸の長さ)がわかる
横軸(X)と縦軸(Y)がわかることになるので、
この動画の真ん中のボールみたいに、1度変わるごとにX(横)とY(縦)がわかって、ちょうどまん丸に動くようになります。
- 高さ(Y軸)を r(円の半径)(今回は100) かける サイン(sinθ) で出して、
- 横(X軸)を r(円の半径)(今回は100) かける コサイン(cosθ) で出しています。
角度が1ずつ変わる事で、この動画みたいな動きになります。
三角関数の応用 波の表現に使われます
実は『三角関数』は、
- スマホなどで使われている『周波数』
- 地震を表す波形
など、
自然界の『波』を分析するのにとても重宝しています。
関連記事
三角関数をわかりやすくまとめてみて
教科書ではしょっちゅうでてくるのに、
日常生活ではまず使わないとレッテルを貼られているかのような『三角関数』。
実際はこれでもかといわんばかりにいろんな世界で使われているんですが、
なかなかその便利さがわからず、使う機会がなかったのかなぁと思います。
けれど、
『スクラッチ』や『JavaScript(ジャバスクリプト)』などを使って、
プログラミングで『三角関数』を使っているうちに、
多少なりとも身近になるんじゃないかなと思ったりしました。
関連記事:『スクラッチ』で『三角関数』の使い方
余談
サインコサインタンジェントの名前の由来の記事があったので紹介しておきます。
『数学・物理』関係ではこんな記事も読まれています。
1. 【P5.js】初心者向けの動画をリリースしました(プログラミング×数学物理)【Udemy】2. 【ベクトル】をわかりやすくするコツ〜『ベクトル』はただの数値の組み合わせです(4)【P5.js】
3. プログラムで数学も身につく 一石四鳥なクリエイティブコーディング
4. 【三角関数】の使い方〜わかりやすさ重視でまとめてみた【動画あり】
5. 【ラジアン】とは わかりやすくまとめてみた【初心者向け】
6. 【図解】波の用語や動きをプログラムも交えてまとめてみる【数学&物理】
7. 【微分】とは わかりやすくまとめてみた〜めっちゃすごいわり算【初心者向け】
8. 【シグマ(∑)】計算をわかりやすくまとめてみた【エクセルのsum】【初心者向け】
9. 【極座標 】とは【直交座標 】との違いや変換方法についてまとめてみた
10. 【虚数】【複素数】とは わかりやすくまとめてみた【初心者向け】
11. 【指数】とは わかりやすくまとめてみた【初心者向け】
12. 【対数】とは わかりやすくまとめてみた【初心者向け】
13. 順列・組み合わせ・階乗とは わかりやすくまとめてみた【数学】
14. 【確率(加法定理)】とは わかりやすくまとめてみた【初心者向け】
15. 【ベクトル場】と【速度ベクトル】とは わかりやすく【ドラクエのすべる床】
↓ ここから下は物理関連
1. プログラムで【加速度】をわかりやすくするために実際に動かしてみる(5)【P5.js】
2. 【流体力学】とは 圧力・密度・浮力をまとめてみた【初心者向け】
↓ ここから下はちょいムズカシイ
1. 【ネイピア数】とは わかりやすくまとめてみた【自然対数の底(e)】
2. 【ベクトル解析 勾配(grad)】わかりやすくまとめてみた
3. 【ベクトル解析 発散(div)】わかりやすくまとめてみた
4. 【テイラー展開】をわかりやすくまとめてみた【おすすめ動画あり】
『クリエイティブコーディング』関係ではこんな記事も読まれています。
1. 【P5.js】初心者向けの動画をリリースしました(プログラミング×数学物理)【Udemy】2. 【JavaScript】初心者向けの動画をリリースしました【Udemy】
3. プログラミング実況をやってみた その1【P5.js】
4. 【P5.js】遊ぶようにプログラムできるクリエイティブコーディング〜はじめのいっぽ〜(1)
5. 移動・回転・拡大縮小を覚えると表現に幅がでてきます(2)【P5.js】
6. 【CSS】色の指定なら『RGB』より『HSL』の方が使いやすい件〜ランダムで使いたい(3)【P5.js】
7. 『ベクトル』の使い方のコツ〜『ベクトル』はただの数値の組み合わせです(4)【P5.js】
8. プログラムで【加速度】【速度】の使い方をわかりやすく (5)【P5.js】
9. プログラムの【配列】をわかりやすく『ゴディバ』で例えてみる(6)【P5.js】
10. プログラムの関数をわかりやすく使ってみる〜自動販売機に例えてみる〜(7)【P5.js】
11. プログラムで色や大きさをランダムにして遊んでみる(8)【P5.js】
12. 【3Dプログラム】初心者にオススメな方法はこれ(9)【P5.js】
13. プログラムで図形の描き方~頂点と【バラ曲線】を使って〜 (10)【P5.js】
14. 【三角関数】をプログラムで使う方法をまとめてみた(11)【P5.js】
15. プログラムで数学も身につく 一石四鳥なクリエイティブコーディング
アオキのツイッターアカウント。

















この記事へのコメントはありません。