『当たり』。なんていい響きなんでしょう。
『当選』。なんていい響きなんでしょう。
- 『チョコボール』にしろ、
- 『ブラックモンブラン』にしろ、
- 『ロト6』にしろ、
- 『年末ジャンボ宝くじ』にしろ、
って事で、
『当たる』か『当たらないか』の2択の場合の計算方法を、
まとめてみることにしました。
当たるか当たらないかを計算する方法
お題はなんでもいいんですが、
今回は『ブラックモンブラン』で当たる確率を計算してみることにします。

『10点当たり』とか『50点あたり』とか、
『当たり』にもいくつか種類があるんですが、
今回はシンプルに、
『当たる』か『当たらない』かの2択として、
5本のうち1本は当たりが入っていると想定してみます。
- 『当たる』確率・・ 1/5
- 『当たらない』確率・・1 – 1/5 で 4/5
ですね。
当たりが出る確率を計算したい 確率変数とは
例えば4回『ブラックモンブラン』を買うとして、
『当たり』をひく回数をXと表すと、
- 1回も当たらない・・あたりは0本
- 4回とも当たる・・あたりは4本
というわけで、
X = 0, 1, 2, 3, 4
と、5通りの可能性がでてきます。
『当たり』がでるパターンの事を、
『確率変数(かくりつへんすう)』といいます。
例えば4回買って2回『当たり』の場合は、
P(X=2) と表現するようです。
- 確率変数・・英語でProbability variable(プロバビリティ バリアブル)
今回の場合でいうと、
4回買って当たり0本の場合もあれば、
4回買って4本とも当たる可能性もありえるので、
『確率変数』は、
- P(X=0)
- P(X=1)
- P(X=2)
- P(X=3)
- P(X=4)
と、5パターンありえることになります。
当たりが出る確率を計算する方法 『ベルヌーイ試行』
今回のように、
『当たる』か『当たらない』かなど、
2つの選択肢で確率を考えることを、
『ベルヌーイ試行』といいます。
- ベルヌーイ試行・・英語でBernoulli trial(ベルヌーイ トライアル)
-
ヤコブ・ベルヌーイ・・1654~1705 スイスの数学者・科学者
計算式はこう。
$$p^r \times (1 – p)^{n-r} \times {}_n \mathrm{ C }_r $$
- p・・確率
- n・・繰り返す数
- r・・当たりを引く数
-
$$p^r $$・・r回 当たる
- $$(1 – p)^{n-r}$$・・(n-r)回当たらない
- $${}_n \mathrm{ C }_r $$・・n回中どのr回で当たるか
『組み合わせ』の関連記事
この計算式を、
- P(X=0)
- P(X=1)
- P(X=2)
- P(X=3)
- P(X=4)
の5つのパターンでそれぞれ計算すれば、
それぞれの確率がわかるという事になります。
手計算で頑張ってもいいんですが、
今回は、
『Excel(エクセル)』
『Python(パイソン)』
それぞれの機能を使って計算してみたいと思います。
当たりが出る確率を計算する 『二項分布』をExcelで
『当たり』か『当たらない』かのように、
2択で分けられる場合の表やグラフの事を、
『二項分布(にこうぶんぷ)』といいます。
英語だと、
『Binomial Distribution』(バイノミアル ディストリビューション)
という呼び名になります。
『Excel(エクセル)』だと、
『二項分布』の英語名を省略した『BINOM.DIST』関数を使います。
引数は4つ。
- 値・・当たりの本数(r)
- 実施する回数・・(n)
- 当たる確率・・(p)
- false・・確率質量関数(trueで累積分布関数)
5つのパターンをそれぞれ計算して、
- P(X=0)
- P(X=1)
- P(X=2)
- P(X=3)
- P(X=4)
値と計算した範囲を選びつつ、
グラフの挿入→散布図 とするとこんなグラフが描けます。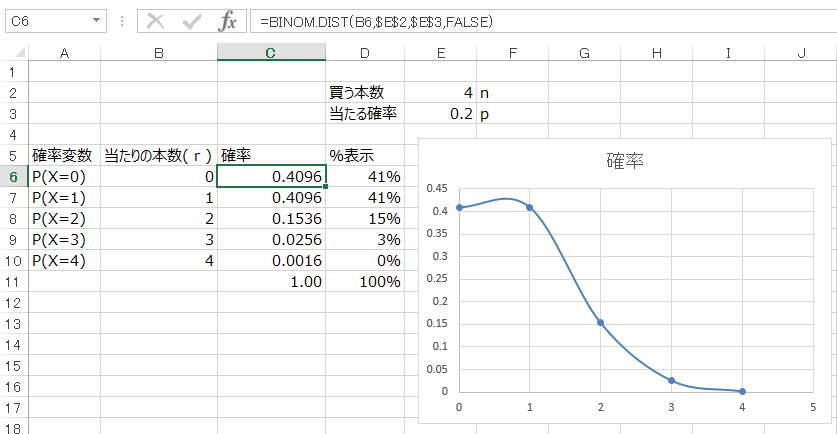
試しに『ブラックモンブラン』を買う回数(n)を 4回→10回にするとこう変わります。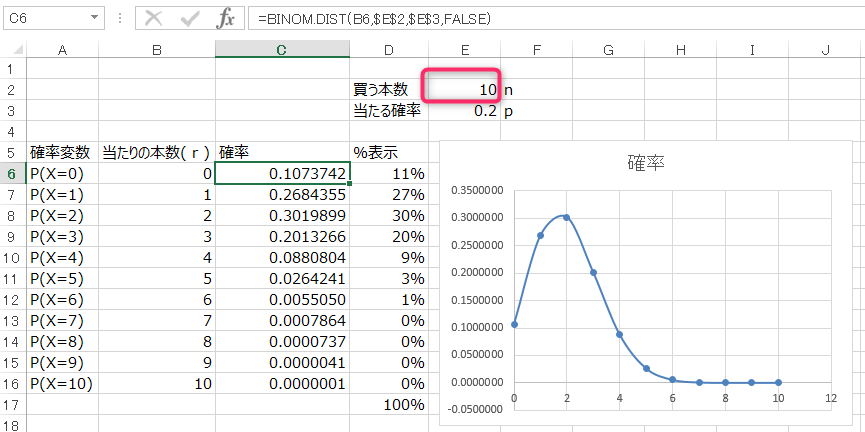
試しに当たる確率(p)を 0.2 → 0.5 (50%) にするとこう変わります。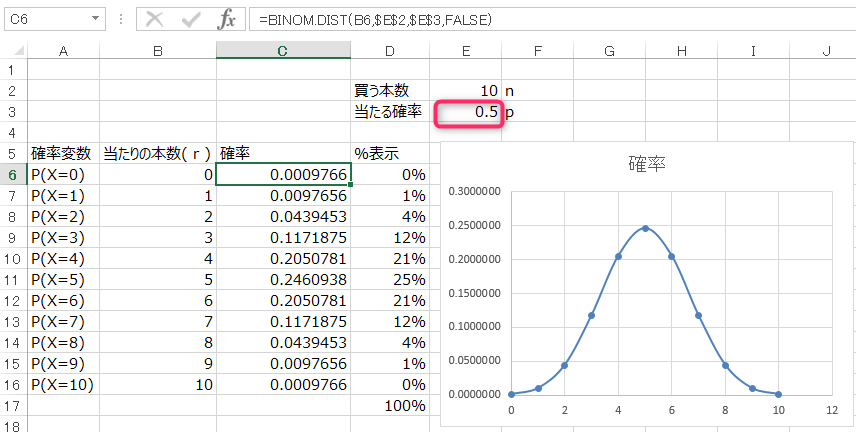
どうやら当時の『ベルヌーイ』さんが、
『二項分布』をいろいろと試しているうちに、
『正規分布』の法則も見つけていったそうです。
『正規分布』の関連記事
当たりが出る確率を計算する 『二項分布』をPythonで
『Python(パイソン)』ではいくつか描画する方法がありますが、
今回は計算ライブラリ『scipy(サイパイ)』の中の『binom』関数を使ってみます。
# インポート
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom # 二項分布の関数
# 確率
p = 0.5
# 試行回数
N = 10
# 試行回数中の発生回数 (配列)
k = np.arange(N+1)
# グラフにプロット
# pmfは確率質量変数 probability mass function の略
fig, ax = plt.subplots(1,1)
plt.plot(binom.pmf(k, N, p))
# グラフ表示
ax.set_xlabel('number')
ax.set_ylabel('probability')
ax.set_title('binomial distribution')
ax.set_ylim((0,0.30))
コマンドを実行すると、こんなグラフが表示されます。
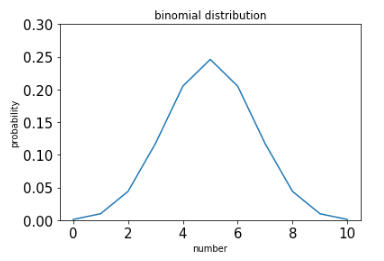
環境設定の参考記事
当たりが出る確率の計算をまとめてみて
- 『当たる』か『当たらない』か
- 『売れる』か『売れない』か
- 『丁』か『半』か
- 『好き』か『好きじゃない』か
まるで花占いみたいに、2択で判断できる確率をまとめてみるうちに、
- ベルヌーイ試行
- 確率変数
- 二項分布
などといった統計学の専門用語に触れる事になりました。
計算方法はちょっとややこしいですが、
『エクセル』なり『Python』なりの力を借りれば、
たくさんのケースでもさくっと計算できるので、
うまく使いこなして、一番いい確率を見計らって勝負をかけたいもんです。
『統計学』関係ではこんな記事も読まれています。
1. 【分散】【標準偏差】とは わかりやすくまとめてみた【ExcelとPython】2. 【正規分布】とは わかりやすくまとめてみた【ExcelとPython】
3. 【確率】当たりがでる確率を計算する方法【二項分布】【Excel/Python】
4. 順列・組み合わせ・階乗とは わかりやすくまとめてみた【数学】
5. 【確率(加法定理)】とは わかりやすくまとめてみた【※初心者向け】
6. 【条件付き確率】とは わかりやすくまとめてみた
アオキのツイッターアカウント。



















この記事へのコメントはありません。