『3Dプログラミング』に取り組むうちに目にするようになってきた『ベクトル解析』。
『3Dプログラミング』に限らず『工学系』の業界なら必須とも言われていて、『ベクトル解析』には3つ種類があります。
- 勾配(grad)
- 発散(div)
- 回転(rot)
この記事では『発散(はっさん)』についてまとめています。
ベクトル解析 発散(div)をわかりやすく イメージは水流
『発散(はっさん)』は、ストレス発散という言葉があるように、
『散らばる』というような意味になります。
- 発散(はっさん)・・英語でdivergence(ダイバージェンス)。略してdiv(ディブ)
数学で考えるときは、水の流れ、『水流』で考えるとわかりやすいそうで。
図にするとこんなイメージでしょうか。
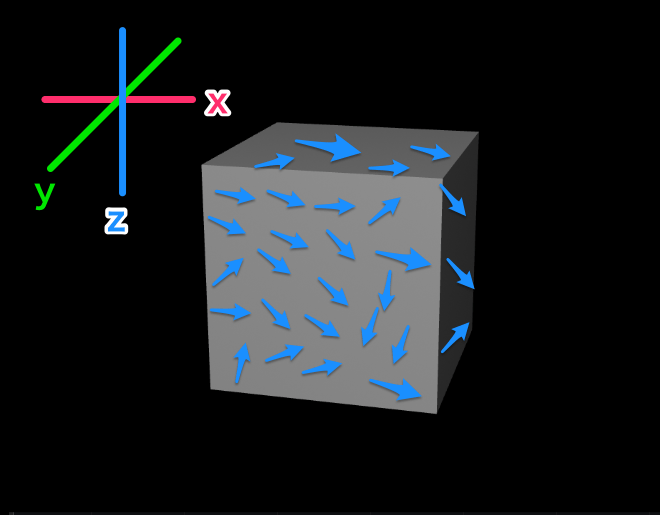
『X』『Y』『Z』の3軸があって、
その中で『水流』がザバーンと動いていると。
1点1点でそれぞれ方向や流れるスピードが違うと。

ベクトル解析 発散(div)をわかりやすく 湧き出しと吸い込み
『発散(div)』には独特の2つの考え方があります。
- 湧き出し
- 吸い込み
こちらも図をつくってみました。
3D空間の1点に注目して、その周りを小さな直方体で囲ったとします。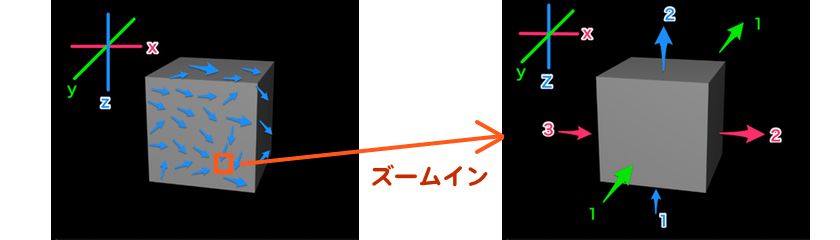
- X軸・・左側から3入って、右側に2出ていく
- Y軸・・手前側から1入って、奥側に1出ていく
- Z軸・・下側から1入って、上側に2出ていく
というケースの場合。
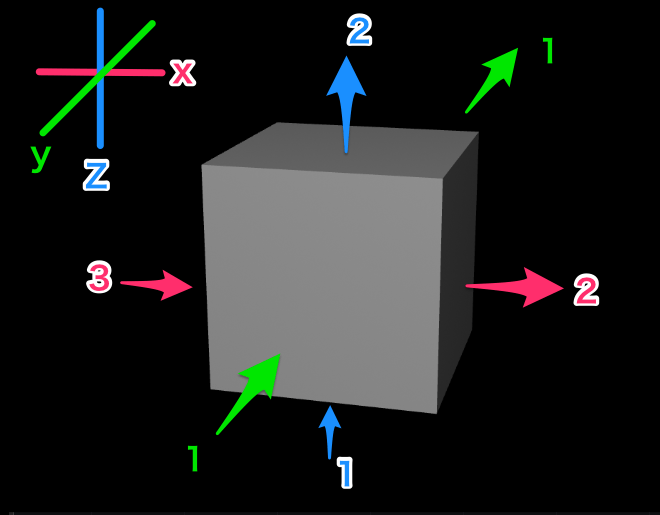
- 出ていった量(流出量)は (2+1+2) = 5
- 入ってきた量(流入量)は (3+1+1) = 5
『流出量』 – 『流入量』 = 0 になるので、
『湧き出し』も『吸い込み』も発生していないという事になります。
もし『流出量』の方が多かったら、
立方体の中で水が増えていることになるので『湧き出し』といい、
もし『流入量』の方が多かったら、
立方体の中で水が減っていることになるので『吸い込み』といいます。
ベクトル解析 発散(div)をわかりやすく 流出量-流入量を計算してみる
先ほどと同様、3D空間の1点を注目して、その周りを小さな直方体で囲ったとします。
とっても小さな直方体なので、それぞれΔx、Δy、Δzと表現します。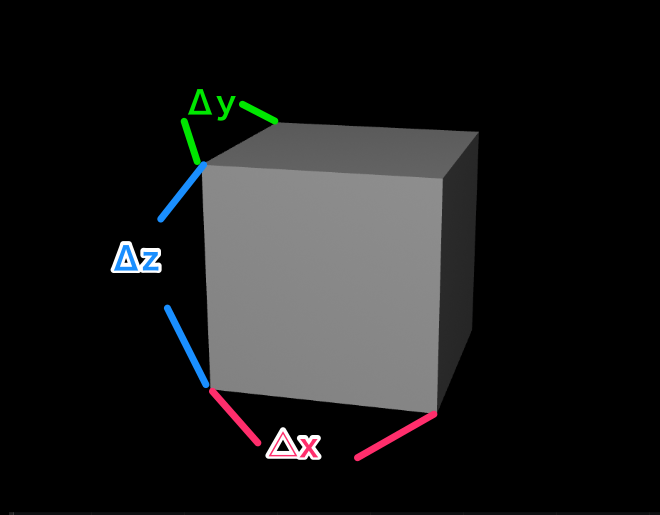
1点とはいえ流れがあるので『ベクトル』で考える必要があって、
1点(P)(x,y,z)を、X軸、Y軸、Z軸それぞれで分解して考えます。
- Vx = (Vx(x, y, z), 0, 0)
- Vy = (0, Vy(x, y, z), 0)
- Vz = (0, 0, Vz(x, y, z))
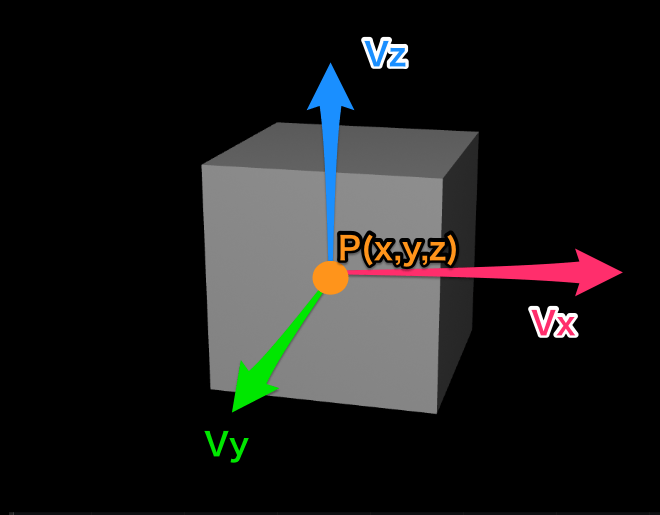
3軸あるのでそれぞれ計算するのですが、まずは代表して横軸(X軸)に注目します。
- 横軸(X軸)・・流出量(濃いピンク) – 流入量(薄い紫)
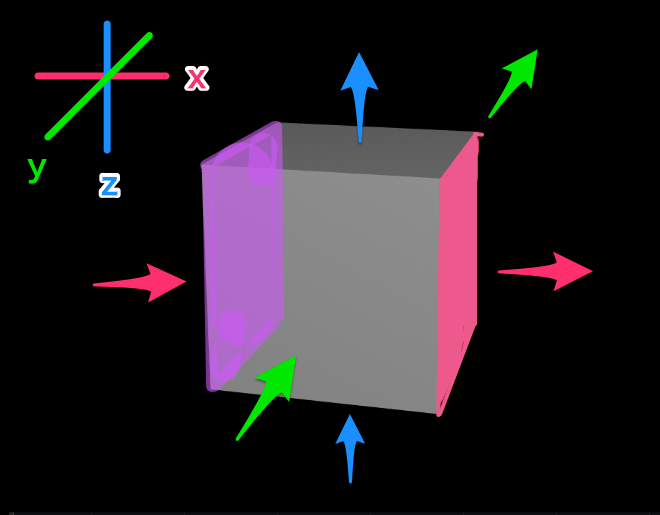
水流の速さが『Vx(x, y, z)』になります。
流入量の位置を『x』、流出量の位置を『x + Δx』 として、
ピンクの面積は『ΔyΔz』になるのでこうなります。
- 流出量 ・・ Vx(x + Δx,y,z)ΔyΔz
- 流入量 ・・ Vx(x,y,z)ΔyΔz
式にすると、流出量 – 流入量 なので、
$$ Vx(x + \Delta x,y,z)\Delta y\Delta z – Vx(x,y,z)\Delta y\Delta z $$
になります。
『x』で『偏微分』できるようにこう書き換えます。
$$ \frac{Vx(x + \Delta x , \Delta y, \Delta z )- Vx(x , \Delta y, \Delta z ) }{\Delta x}\Delta x \Delta y \Delta z $$
『Δ』はほとんどゼロということで『d』に書き換えつつ、『x』で『偏微分』するとこうなります。
$$ \frac{\partial Vx}{\partial x}dxdydz$$
・偏微分・・xならxだけに着目し、yやzを定数(0など)と考えて、xだけ微分する方法。yならyだけ微分。zならzだけ微分。
微分についての関連記事
X軸だけではなく、Y軸、Z軸もそれぞれ計算するとこうなります。
$$ \frac{\partial Vx}{\partial x}dxdydz + \frac{\partial Vy}{\partial y}dxdydz + \frac{\partial Vz}{\partial z}dxdydz$$
『dxdydz』が同じなのでくくります。
$$ (\frac{\partial Vx}{\partial x} + \frac{\partial Vy}{\partial y} + \frac{\partial Vz}{\partial z })dxdydz$$
『dxdydz』は直方体の体積になるので、
『dxdydz』で割って、単位体積あたりの値ということにします。
$$ \frac{\partial Vx}{\partial x} + \frac{\partial Vy}{\partial y} + \frac{\partial Vz}{\partial z }$$
ベクトル解析 発散(div)をわかりやすく 発散(div)の式
$$ \frac{\partial Vx}{\partial x} + \frac{\partial Vy}{\partial y} + \frac{\partial Vz}{\partial z }$$
は湧き出し量の強さということになり、
この式が、
ベクトル場$$ div\overrightarrow{V} $$の『発散(div)』として定義されています。
3次元版
$$ div\overrightarrow{V} = \frac{\partial Vx}{\partial x} + \frac{\partial Vy}{\partial y} + \frac{\partial Vz}{\partial z } $$
XYの2軸版もあります。
2次元版
$$ div\overrightarrow{V} = \frac{\partial Vx}{\partial x} + \frac{\partial Vy}{\partial y} $$
『湧き出し』と『吸い込み』の話に戻ると、
- $$ div\overrightarrow{V} = 0 $$ なら湧き出しはなくて、
- $$ div\overrightarrow{V} > 0 $$ なら湧き出しがある
- $$ div\overrightarrow{V} < 0 $$ なら吸い込みがある
という判定に使えるようで、
他にも、『膨張』と『圧縮』などの判断にも使えるようです。
ベクトル解析 発散(div) わかりやすく 勾配(grad)と発散(div)の関係
『ベクトル解析』3兄弟はそれぞれ関連があるそうで、
今回は、『勾配(grad)』と『発散(div)』の関係をば。
『勾配(grad)』では『$$\nabla$$(ナブラ)』という演算子が使われているのですが、
$$ \nabla = (\frac{\partial}{\partial x},\frac{\partial}{\partial y}, \frac{\partial}{\partial z}) $$
参考記事
実は$ div\overrightarrow{V} $もまた、
『$\nabla$(ナブラ)』を使って表現する事ができます。
$$ div\overrightarrow{V} = \frac{\partial Vx}{\partial x} + \frac{\partial Vy}{\partial y} + \frac{\partial Vz}{\partial yz} $$
$$ = (\frac{\partial}{\partial x} + \frac{\partial}{\partial y} + \frac{\partial}{\partial yz})\cdot(Vx, Vy, Vz) $$
$$ = \nabla\cdot\overrightarrow{V} $$
また、『発散(div)』の中に『勾配(grad)』を含める式もあるようです。
$$ div(grad f) = \nabla\cdot\nabla f = \nabla ^2 f $$
$$ \nabla ^2 $$は$$ \nabla \cdot \nabla $$のことで、
『$$\Delta$$(ラプラシアン)』という演算子で表すこともできます。
$$ \Delta = \nabla ^2 = \nabla \cdot \nabla $$
$$ \Delta = (\frac{\partial }{\partial x}, \frac{\partial }{\partial y}, \frac{\partial }{\partial z})\cdot(\frac{\partial }{\partial x}, \frac{\partial }{\partial y}, \frac{\partial }{\partial z}) $$
$$ = \frac{\partial^2 }{\partial x^2} + \frac{\partial^2 }{\partial y^2}+ \frac{\partial^2 }{\partial z^2} $$
『内積』なので『+』になります。
ベクトル解析 発散(div) わかりやすく おすすめ動画
おすすめ動画はおなじみの、教育系Youtuberヨビノリたくみさん。
全体的にわかりやすいものの、
『2変数のテイラー展開』のところがぱっとわからなかったので、引き続き鍛錬したいと思います。
テイラー展開の参考記事(1変数版)
ベクトル解析 発散(div) わかりやすくまとめてみて
『3Dプログラミング』に取り組むにつれ、
『ベクトル解析』をちょくちょく目にするようになってきました。
『チームラボ』の本にもがっつり『ベクトル解析』が書かれています。
(正確には『ベクトル解析』が前提の『ナビエストークス』方程式が書かれています。さらにムズカシイ・・)
『チームラボ』の『メディアアート』映像。
『ベクトル解析』をしっかりモノにして、キレイで楽しめる映像がつくれたらなと思っています。
PS.
こちらの本を参考にしつつ記事を書きました。読みやすいのでぜひ。
『数学・物理』関係ではこんな記事も読まれています。
1. 【P5.js】初心者向けの動画をリリースしました(プログラミング×数学物理)【Udemy】2. 【ベクトル】をわかりやすくするコツ〜『ベクトル』はただの数値の組み合わせです(4)【P5.js】
3. プログラムで数学も身につく 一石四鳥なクリエイティブコーディング
4. 【三角関数】の使い方〜わかりやすさ重視でまとめてみた【動画あり】
5. 【ラジアン】とは わかりやすくまとめてみた【初心者向け】
6. 【図解】波の用語や動きをプログラムも交えてまとめてみる【数学&物理】
7. 【微分】とは わかりやすくまとめてみた〜めっちゃすごいわり算【初心者向け】
8. 【シグマ(∑)】計算をわかりやすくまとめてみた【エクセルのsum】【初心者向け】
9. 【極座標 】とは【直交座標 】との違いや変換方法についてまとめてみた
10. 【虚数】【複素数】とは わかりやすくまとめてみた【初心者向け】
11. 【指数】とは わかりやすくまとめてみた【初心者向け】
12. 【対数】とは わかりやすくまとめてみた【初心者向け】
13. 順列・組み合わせ・階乗とは わかりやすくまとめてみた【数学】
14. 【確率(加法定理)】とは わかりやすくまとめてみた【初心者向け】
15. 【ベクトル場】と【速度ベクトル】とは わかりやすく【ドラクエのすべる床】
↓ ここから下は物理関連
1. プログラムで【加速度】をわかりやすくするために実際に動かしてみる(5)【P5.js】
2. 【流体力学】とは 圧力・密度・浮力をまとめてみた【初心者向け】
↓ ここから下はちょいムズカシイ
1. 【ネイピア数】とは わかりやすくまとめてみた【自然対数の底(e)】
2. 【ベクトル解析 勾配(grad)】わかりやすくまとめてみた
3. 【ベクトル解析 発散(div)】わかりやすくまとめてみた
4. 【テイラー展開】をわかりやすくまとめてみた【おすすめ動画あり】
アオキのツイッターアカウント。


















この記事へのコメントはありません。